ECONOMICS WORKING PAPER SERIES

ESTIMATED TARIFF EQUIVALENTS OF SERVICES NTMS

Lionel Fontagné
Cristina Mitaritonna
José E. Signoret

Working Paper 2016-07-A

U.S. INTERNATIONAL TRADE COMMISSION

500 E Street SW

Washington, DC 20436

July 2016

Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research.

Estimated Tariff Equivalents of Services NTMs
Lionel Fontagné, Cristina Mitaritonna, and José E. Signoret
Office of Economics Working Paper 2016-07-A
July 2016

Lionel Fontagné

Paris School of Economics $—$ University Paris 1
Centre d’Études Prospectives et d’Informations Internationales (CEPII)

Cristina Mitaritonna

Centre d’Études Prospectives et d’Informations Internationales (CEPII)

José E. Signoret

U.S. International Trade Commission, Office of Economics

Jose.Signoret@usitc.gov

1. Introduction

As previous trade liberalizations have lowered tariffs worldwide, nontariff measures, or NTMs, remain as the most visible issues to be addressed. This is especially true in the case of services, where measures likely to affect services trade do not involve tariffs. In fact, significant trade agreements currently under negotiation, such as a number of mega-regional free trade agreements and an ambitious multilateral Trade in Services Agreement (TISA), particularly aim at reducing services NTMs. The result is that there is wide interest from both policy makers and economists in understanding the impact of these measures.

Unfortunately, quantifying the restrictiveness of NTMs for services has proven to be difficult. The main limitation has been the lack of comprehensive data, whether trade, policy, or microeconomic data.

Gathering data on actual policies has been especially challenging. Up until recently, information on the regulatory environment affecting services trade was not available for a wide range of countries, nor was it necessarily collected in a consistent fashion. Efforts by the World Bank (Borchert, Gootiiz, and Mattoo, 2012) and the Organisation for Economic Co-operation and Development (OECD) (Geloso Grosso et al., 2015) to collect this information and to develop services trade restrictiveness indexes as “summary statistics” of the level of restraints have been an important advance. By themselves, however, these indexes (often called STRIs) have no obvious economic meaning, and they would require some empirical analysis to associate them with trade costs.

One strand of the literature has used the STRI information to explain the observed international variation in price-cost margins, conditional on other firms and country factors. The pioneering work of Dee (2004) and Dihel and Sheperd (2007) provide early examples of this work. Fontagné and Mitaritonna (2013) conduct a similar analysis and stress the limitations of this approach. First, qualitative information must be arbitrarily transformed into a quantitative measure of the restrictiveness of each measure considered individually. Second, this approach is very data-consuming with respect to both microeconomic evidence and the determinants of price-cost margins in services sectors. As a consequence, estimated coefficients on restrictiveness indexes have to be used out of sample. This is a huge restriction, because the distribution of firms or markups within a given sector necessarily diverges across countries $—$ even more so when countries at different levels of development are considered.

Jafari and Tarr (2015) nevertheless employ this method, using the World Bank STRI, to compute ad valorem equivalents (AVEs) for a large set of countries. Other recent research using STRI information has relied on gravity modeling. The analyses by van der Marel and Shepherd (2013) and Riker (2014) using the World Bank index, or by Nordås and Rouzet (2015) using the OECD STRI, are examples of gravity models that incorporate STRI values in their econometric specifications. Finally, Gooris and Mitaritonna (2015) exploit the ordinal nature of restrictiveness levels to assess the trade impact of a measure in place in a given country for a given sector. They conclude that the trade-impeding effects of restrictions may be nonlinear.

Although available for a large set of countries, data on services trade flows are much more aggregated than data on merchandise trade. But even if information on trade in services is limited, it is possible to use it to compute AVEs of the effects of barriers to trade in services on the quantities (instead of the prices) of traded services. Of course, bilateral trade data are not available for all possible trading partners, and the existing gaps have to be filled via estimation methods with reconstructed data. Sources of such data may include the services trade data in the Global Trade Analysis Project (GTAP) and other global databases.

Fontagné, Guillin, and Mitaritonna (2011) illustrate how to carry out such an analysis and then compare the results obtained with different identification strategies and different datasets. Their analysis uses a reduced form of the gravity approach to estimate services trade without relying on STRI information. The tariff equivalents are then inferred by comparing the inward multilateral resistance term for each country with that of a benchmark country. In this note, we build on this approach and provide AVEs of restrictions on trade in services for 117 countries in 2011. This estimation uses GTAP data, making it consistent with modeling efforts by several trade economists.

The econometric estimation used is this note is a practical approach that can be applied to obtain AVEs even for services sectors that do not line up with STRI sectors and for years for which there is no STRI information. It also bypasses the need for data on price-cost margins within sectors and countries. In fact, as in this note, estimates across many countries and sectors can be updated as more recent trade data become available. Further, this approach is not susceptible to how regulations are scored and how these scores are then weighted in forming the STRI.

Our results compare with those of Fontagné, Guillin, and Mitaritonna (2011), who used GTAP data for the year 2004. We use the same method, although the set of countries for which we have estimated the equivalents is larger. For the sake of comparison, we also provide results obtained with Fontagné, Guillin, and Mitaritonna’s original sample of countries, but for 2007 and 2011. In the latter case, we estimate and compute AVEs on the reduced sample of 64 countries.

The reader, however, must be aware that the estimated AVEs are only rough estimates of the restrictiveness of regulations on services. Our approach is likely to pick up trade cost factors beyond policy restraints, so that the tariff equivalent results may reflect a broad range of “frictions.” And although these estimates can easily be incorporated into large-scale trade models, they are not likely to be fully actionable. Berden et al. (2009), for instance, consider that, overall, 50 percent of NTM AVEs in goods and services in transatlantic trade may be actionable $—$ and even that 50 percent is probably an ambitious goal. Evidence on this question has to be taken from trade negotiators or specialists in the concerned sectors, and it is beyond the scope of this note. Notice, however, that we systematically benchmark our estimations against a country with a zero AVE, although regulations on services may be present in this country. We are not measuring the cost of regulations, but rather their restrictiveness for trade flows.

The rest of this note is organized as follows. Section 2 presents the empirical approach used. Section 3 describes the data and econometric identification. Results are presented in section 4. The last section concludes the discussion. The full set of updated results is included with this note as an Excel file.

2. Empirical Framework

Many methodological issues can arise when using the gravity approach to construct AVEs of barriers to trade in services. First, the distribution of residuals of the estimated equation is sensitive to problems of specification and omitted variables, which affects the estimation of tariff equivalents. Hence it may be preferable to rely on a strategy based on country fixed effects. Second, an assumption must be made on the elasticity of substitution used to transform the parameter estimates to AVEs. The value of the equivalents is highly sensitive to this assumption, although the ranking of the restrictiveness of countries’ regulations in a given sector is not. These constraints led us to choose a simple identification strategy in tackling unobserved dimensions (like restrictiveness) in the importing country. Fontagné, Guillin, and Mitaritonna (2011) show that identifying the quantity effect of barriers to trade in services by relying on the GTAP database provides highly usable measurements of AVEs. We have built on this approach.

Our first step is to estimate a gravity equation in a cross-section relying on partially reconstructed data. In the GTAP database on trade in services for 2011, based on OECD data, the gaps for missing data are filled and then the database reconciled. There are accordingly two issues here: we rely on a very specific set of data as regards trade in services, namely the GTAP dataset of trade in services, while deriving estimates only with cross-sectional methods. These issues are not major obstacles, however, as illustrated by Fontagné, Guillin, and Mitaritonna (2011): while the latter study used alternative data sources and a panel database, the results were shown to be not too different.

3. Data and identification

We make use of a relative small set of data sources. The main source of data used in this paper remains the GTAP database, which provides bilateral trade in services for 15 services sectors for the year 2011: air transport (atp), communications (cmn), construction (cns), dwellings (dwe), electricity (ely), gas distribution (gdt), insurance (isr), other business services (obs), other financial intermediation (ofi), other government services (osg), other transport (otp), recreational services (ros), trade (trd), water (wtr), and water transport (wtp). This dataset has more countries than the GTAP database for the year 2004 that was used in Fontagné, Guillin, and Mitaritonna (2011). For sake of comparison, we provide tariff equivalents computed using alternatively the (reduced) sample of countries found in Fontagné, Guillin, and Mitaritonna (2011) and the enlarged sample of countries available in the GTAP database for the year 2011. For sake of comparison with Fontagné, Guillin, and Mitaritonna (2011), we keep the decomposition into the following services sectors: cmn, cns, obs, trn, trd, isr, ofi, and osg. In this listing, trn stands for transport, which includes the three transport sectors (atp, wtp, and otp). As in the reference article, wtp is also kept separately.

The gravity variables were obtained from the Centre d’Études Prospectives et d’Informations Internationales (CEPII) and updated for as necessary using data obtained from the World Bank.

For each services sector, the estimating equation used in the current analysis takes the form:[1]

$x_{i j} = c + 0.8 y_{j} + α_{i j} d i s t_{i j} + β_{i j} D_{i j} + γ_{i} + γ_{j} + ε_{i j}$ (1)

Where $x_{i j}$ represents the log of exports from country $i$ to partner $j$ . Trade costs other than regulations between $i$ and $j$ are proxied by $d i s t_{i j}$ , the log of their bilateral distance. The vector $D_{i j}$ contains bilateral trade determinants common in the gravity literature, including distance, contiguity, a colonial relationship, a common language, engagement in a free trade agreement, etc., here controlled by dummy variables. We include exporter $γ_{i}$ and importer $γ_{j}$ fixed effects to estimate the usual multilateral resistance terms. Since we do not have time series, gross domestic products (GDPs) should collapse in these fixed effects. However, we would like to clean the importer fixed effect from the importer GDP, in order to capture only the degree of restrictiveness of trade in this importing country. We constrain the coefficient for expenditures in the importing country to 0.8, to normalize exports by the potential size of the market.[2] The last term represents an error term.

The last step involves the derivation of the tariff equivalents. There are two ways to compute the average protection applied by each importer: either from the estimated residuals (as in Park 2002), or else from the importer fixed effect coefficients. Although the importer fixed effect coefficient captures something larger than the protection itself, it is preferable to residuals. Not only do the latter contain mixed information other than protection, but their magnitude and goodness largely depend on the fit of the equation performed.

We need to examine the underlying theory in more depth to understand the assumptions involved in relying on the canonical gravity equation derived by Anderson and van Wincoop (2003) in order to compute the revealed trade barriers of country $j$ .

Exports from country $i$ to country $j$ accounting for a share $S_{j}$ of world income can be expressed as a simple function of the product of their GDP and of trade costs.[3] Noting $y$ as GDP (subscript $w$ for world), $τ$ trade costs (the power of the AVE) and $σ$ the elasticity of substitution, we have the following expression for the bilateral trade flows $x_{i j}$ :

$x_{i j} = \frac{y_{i} y_{j}}{y_{w}} {(\frac{τ_{i j}}{Π_{i} P_{j}})}^{(1 - σ)}$ (2)

Where $P_{j}$ refers to the price index of the demand function in $j$ and $Π_{i}$ to a term which transmits the effect of an increase in the level of import restrictiveness for non-j services importers that stimulates exports from i to j:

$Π_{i} = {(\sum_{j} S_{j} (τ_{i j} / P_{j}))}^{1 / (1 - σ)}$ (3)

How the estimated equation fits in is simple. In our model (equation 1), $y_{j}$ is observed, $y_{i} Π_{i}^{(σ - 1)}$ is captured by the exporter fixed effect, $P_{j}^{(σ - 1)} τ_{i j}^{(1 - σ)}$ by the importer fixed effect, and $y_{w}$ is in the constant.

We must now assume that the regulation on a services sector in j has the same impact on exports for all affected partners i, hence $τ_{i j} = τ_{j}$ and that the impact on $Π_{i}$ of changes in $τ_{j}$ is small enough to be neglected, as a result of a small enough $S_{j}$ (the weight of the destination country expenditure in j over the world production).

As regulations cannot be directly observed, one should compare the actual trade with a theoretical situation (subscript free), excluding any trade costs associated with restrictive regulations on trade in services in the destination j,[4] hence computing the theoretical ratio of $x_{i j} / x_{i j}^{f r e e}$ , which after simplification is equal to $α_{j}^{σ - 1} τ_{i j}^{1 - σ}$ , with $α \equiv P_{j} / P_{j}^{f r e e}$ . If we assume that $P_{j}$ and $P_{j}^{f r e e}$ are similar, then the $α$ term can be omitted.

As the theoretical value $x_{i j}^{f r e e}$ cannot be observed either, there is a need to define a benchmark country, supposed to be the free trader of the sample. The benchmark is the country with the highest positive difference between the actual and predicted average import values. All calculations must be made relative to this benchmark, and one must normalize the ratio of actual to predicted trade for each importing country by the same ratio computed for the benchmark. Under the assumptions made above and after summation over j’s partners, the log of this double ratio therefore becomes the difference in the logs, as follows:

$\ln {(1 + t_{j})}^{1 - σ} = γ_{j} - γ_{0}$ (4)

Where $γ_{0}$ is the highest importer fixed effect coefficient.

From equation 1 we get the estimation of $\ln {(1 + t_{j})}^{1 - σ}$ , however the specific values of the tariff equivalents ( $t_{j}$ ) will also depend on the elasticity of substitution $σ$ that is not estimated in the model, but needs to be assumed.

Following Fontagné, Guillin, and Mitaritonna (2011) and for sake of comparison, we use the assumption that $σ = 5.6$ . A higher $σ$ provides lower AVEs, and vice versa. The relative ranking among the different countries, however, is not sensitive to the assumed value of the elasticity of substitution.

4. Results

We now show the results of the estimated equations using data for 2011 and the largest set of countries (117) and for nine sectors of services, disregarding water, electricity, gas manufacture and distribution, recreational and other services, and dwellings. As noted, air transport and other transport are not considered separately, but included in all transports (trn), a category that also includes water transport. Distance has a negative impact on trade in services, because distance is a proxy of many other dimensions besides transport costs (e.g., communication costs). Contiguity and a colonial relationship facilitate trade in services, because of the existence of business networks and the fact that certain services (such as construction) are provided cross border. The liberalization of trade in services in Europe shows up in the positive coefficient for Europe, and the same conclusion holds for NAFTA, notwithstanding the lower integration in North America. Again, business services and the presence of affiliates of foreign companies may play a role here. What is observed in Europe or North America contrasts sharply with the observed parameter estimate for Latin America.

Most important for us, however, are the importing country fixed effects, as explained above. We now rely on these fixed effects to compute the AVEs, using an elasticity of substitution of 5.6. Results are shown in table 2 for the top five more open countries and the top five more protective ones, for each category of services. We report in parentheses in table 2 also the fixed effect of the best performer, so that the estimated AVEs in 2011 can be recalculated using different elasticities of substitutions.

An Excel file with the complete set of results for the 9 sectors and the 117 countries is available with this note. This file does not report results for a limited number of pairs (sector, importer), as the parameter estimates were not significant. This set of unreported pairs corresponds to 7.7 percent of the total number of pairs. In figure 1 we show the distribution of estimated AVEs by services sector for the remaining 92.3 percent of the sector-importer pairs.

For the sake of comparison with Fontagné, Guillin, and Mitaritonna (2011), who computed AVEs for 64 countries in 2004, we perform the same calculation for 2007 and 2011, restricting our estimation of parameters and derivation of tariff equivalents to these 64 countries. Results are provided in the Excel file.

Table 1 Results of estimations for whole GTAP sample of countries, 2011

	cmn		cns	isr	obs	ofi	trd	trn	osg	wtp
Log distance	-0.0398***		-0.0902***	-0.0206**	-0.0672***	-0.0739***	-0.0600***	-0.0318***	-0.0509***	-0.0102
	(0.00820)		(0.0171)	(0.00948)	(0.0100)	(0.0118)	(0.0105)	(0.00909)	(0.00977)	(0.0150)
Contiguity	0.389***		0.292***	0.444***	0.325***	0.370***	0.411***	0.368***	0.407***	0.465***
	(0.0328)		(0.0661)	(0.0378)	(0.0401)	(0.0469)	(0.0416)	(0.0361)	(0.0388)	(0.0607)
Common language	-0.0100		0.0172	-0.00119	-0.0209	-0.0409*	-0.0307	-0.0569***	-0.0135	-0.00993
	(0.0169)		(0.0348)	(0.0196)	(0.0207)	(0.0242)	(0.0217)	(0.0187)	(0.0202)	(0.0313)
Colonial relationship	0.257***		0.177**	0.197***	0.272***	0.266***	0.385***	0.318***	0.295***	0.222***
	(0.0380)		(0.0730)	(0.0436)	(0.0465)	(0.0532)	(0.0482)	(0.0423)	(0.0456)	(0.0681)
ASEAN	-0.0851		0.183	-0.00758	-0.0768	-0.0973	0.00422	-0.115	-0.117	-0.0942
	(0.0818)		(0.157)	(0.0939)	(0.100)	(0.114)	(0.104)	(0.0912)	(0.0982)	(0.146)
Latin America	-0.325***		0.0879	-0.346***	-0.324***	-0.353***	-0.309***	-0.264***	-0.275***	-0.224**
	(0.0508)		(0.113)	(0.0591)	(0.0622)	(0.0730)	(0.0645)	(0.0565)	(0.0609)	(0.0929)
Europe	0.0852***		0.334***	0.218***	0.325***	0.501***	0.502***	0.178***	0.379***	0.317***
	(0.0268)		(0.0523)	(0.0308)	(0.0328)	(0.0377)	(0.0341)	(0.0299)	(0.0322)	(0.0483)
NAFTA	0.809***		-0.758*	0.295	0.533**	0.926***	1.222***	0.703***	0.726***	0.773**
	(0.207)		(0.397)	(0.238)	(0.254)	(0.290)	(0.263)	(0.231)	(0.249)	(0.371)
ANZCERTA	0.143		0.819	0.397	0.0191	0.219	0.370	0.177	0.416	0.472
	(0.354)		(0.678)	(0.407)	(0.434)	(0.495)	(0.449)	(0.395)	(0.426)	(0.633)
Constant	-3.102***		-4.929***	-2.099***	-0.977***	-1.479***	-2.946***	-1.236***	-0.127	-6.659***
	(0.102)		(0.204)	(0.117)	(0.124)	(0.144)	(0.129)	(0.113)	(0.121)	(0.184)
Obs	13,555		12,195	13,380	13,468	12,987	13,428	13,651	13,746	12,877
Importer fixed effects		yes	yes	yes	yes	yes	yes	yes	yes	yes
Exporter fixed effects	yes		yes	yes	yes	yes	yes	yes	yes	yes

Notes: Standard errors in parentheses; *** p<0.01, ** p<0.05, * p<0.1.

Sectors include communication (cmn); construction (cns); insurance (isr); business services (obs); finance (ofi); trade (trd); all transport (trn); other services (osg), comprising education, health, defense and public administration; and water transport (wtp).

Constrained parameter on GDP_j not reported.

Definition of regional dummies as in Park (2002) and Fontagné, Guillin, and Mitaritonna (2011), for the sake of comparison: ASEAN = KHM, MYS, PHL, SGP, THA, VNM, and IND; Latin America = BOL, BRA, CHL, COL, ECU, MEX, NIC, PER, PRY, URY, VEN, and ARG; Europe = AUT, BEL, BGR, CYP, CZE, DEU, DNK, ESP, EST, FIN, FRA, GBR, GRC, HUN, IRL, ITA, LTU, LUX, LVA, MLT, NLD, POL, PRT, ROM, SVK, SVN, and SWE.

Source: Authors’ calculations.

Table 2 Top five free traders and restrictive importers of services, ad valorem equivalent, percent, by sector, 2011

Sector	Top 5 more open countries, by sector					Top 5 more restrictive countries, by sector
cmn	LUX	DNK	BEL	SGP	GBR	BGD	PRY	NAM	BRA	TTO
cmn	0.0 (2.121)	15.1	17.3	19.0	19.5	140.6	143.4	147.5	148.9	172.3
obs	IRL	LUX	SGP	MLT	BEL	ECU	MEX	PRY	BFA	LAO
obs	0.0 (1.769)	8.4	11.8	15.2	16.3	153.6	155.5	157.8	170.7	280.1
trn	SGP	HKG	GRC	DEU	GBR	BFA	BGD	NAM	ZMB	LAO
trn	0.0(1.223)	0.4	6.6	7.3	9.1	79.3	84.2	85.0	85.5	148.0
wtp	GRC	NOR	SGP	HKG	ISR	BFA	PRY	ZMB	BGD	LAO
wtp	0.0(3.667)	7.6	11.3	16.8	20.1	186.3	192.2	194.4	228.2	275.1
cns	AZE	SAU	ZMB	LUX	MYS	BFA	BRA	PRY	BGD	TTO
cns	0.0(2.815)	0.5	6.8	7.7	12.8	161.4	170.6	173.5	180.5	180.6
isr	IRL	LUX	DNK	SGP	MEX	MOZ	RWA	LAO	BLR	TTO
isr	0.0(1.569)	10.8	23.0	23.9	26.5	124.8	130.0	131.8	135.6	170.8
ofi	LUX	IRL	HKG	TWN	MLT	ZMB	GIN	BGD	TTO	LAO
ofi	0.0(2.292)	24.3	31.9	33.6	34.3	165.8	170.9	174.7	196.4	290.6
trd	IRL	SGP	LUX	HKG	NLD	GIN	TGO	BGD	ZMB	LAO
trd	0.0(2.454)	13.5	17.8	21.6	25.9	126.4	131.0	147.9	151.3	217.5
osg	SAU	KWT	BRN	MDG	UKR	ZMB	IND	ETH	TGO	LAO
osg	0.0(1.212)	8.9	35.2	35.6	38.3	107.6	112.9	119.5	129.3	146.3

Note: Numbers in parentheses are estimated fixed effects for the benchmark countries.

Source: Authors’ calculations.

Figure 1 Kernel density of AVEs estimated for 117 countries and 9 services sectors, ad valorem equivalent, 2011

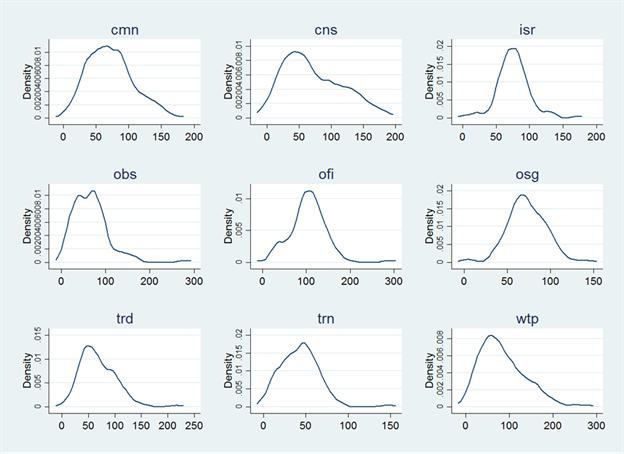
Title: Figure 1 Kernel density of AVEs estimated for 117 countries and 9 services sectors (ad valorem equivalent, 2011) - Description: The figure shows the desity distribution of the AVE estimates across countries for the 9 services sectors (cmn, cns, isr, obs, ofi, osg, trd, trn, wtp). The peak of the distributions range from near 50 percent to near 100 percent.

Source: Authors' calculations.

5. Conclusion

This note derives a set of AVEs of restrictions on cross-border trade in services for 118 countries and 9 sectors, using the GTAP database. The trade data refers to 2011. These equivalents are derived from a quantity method using a gravity model of trade. The econometric estimation is performed sector by sector and the reported AVEs in this note and in the accompanying dataset are based on an assumption of common elasticity of substitution across sectors. Based on the econometric estimation and the elasticity assumption, AVEs for frictions affecting cross-border services trade are large in many sectors. It should be noticed, however, that only a fraction of these estimated costs are reasonably subject to policy changes (or “actionable”) in most circumstances.

References

Anderson, James E., and Eric van Wincoop. “Gravity with Gravitas: A Solution to the Border Puzzle.” American Economic Review 93, no. 1 (2003): 170 $-$ 192.

Berden, Koen, Joseph Francois, Martin Thelle, Paul Wymenga, and Saara Tamminen. “Non-Tariff Measures in EU-US Trade and Investment $—$ An Economic Analysis.” Ecorys. Report for the European Commission, OJ 2007/S 180-219493, 2009. https://trade.ec.europa.eu/doclib/docs/2009/december/tradoc_145613.pdf.

Borchert, Ingo, Batshur Gootiiz, and Aaditya Mattoo. “Guide to the Services Trade Restrictions Database.” World Bank Policy Research Working Paper WPS6108, 2012. https://documents.worldbank.org/curated/en/2012/06/16441094/guide-services-trade-restrictions-database.

Dee, Philippa. “Services Trade Liberalisation in South East European Countries.” Background Paper. Paris: OECD Publishing, January 2004.

Dihel, Nora, and Ben Shepherd. "Modal Estimates of Services Barriers." OECD Trade Policy Papers No. 51. Paris: OECD Publishing, 2007.

Fontagné, Lionel, Amélie Guillin, and Cristina Mitaritonna. “Estimation of Tariff Equivalents for the Services Sectors.” CEPII working paper No 2011 $-$ 24, 2011.

Fontagné, Lionel, and Cristina Mitaritonna. “Assessing Barriers to Trade in the Distribution and Telecom Sectors in Emerging Countries.” World Trade Review 12, no. 1 (2013): 57 $-$ 78. DOI: 10.1017/S1474745612000456.

Geloso Grosso, Massimo, Frédéric Gonzales, Sébastien Miroudot, Hildegunn Kyvik Nordås, Dorothée Rouzet, and Asako Ueno. "Services Trade Restrictiveness Index (STRI): Scoring and Weighting Methodology." OECD Trade Policy Papers No. 177. Paris: OECD Publishing, 2015.

Gooris, Julien, and Cristina Mitaritonna. “Which Import Restrictions Matter for Trade in Services?” Working paper no. 2015-33. Paris: CEPII research center, 2015.

Jafari, Yaghoob, and David G. Tarr. “Estimates of Ad Valorem Equivalents of Barriers against Foreign Suppliers of Services in Eleven Services Sectors and 103 Countries.” World Economy, October 15, 2015. DOI: 10.1111/twec.12329.

Nordås, Hildegunn Kyvik, and Dorothée Rouzet. "The Impact of Services Trade Restrictiveness on Trade Flows: First Estimates." OECD Trade Policy Papers no. 178. Paris: OECD Publishing, 2015.

Park, S.C. “Measuring Tariff Equivalents in Cross-Border Trade in Services.” Trade Working Papers no. 353. East Asian Bureau of Economic Research, 2002.

Riker, David. “Estimates of the Impact of Restrictions on Cross-Border Trade in Services.” U.S. International Trade Commission. Office of Economics Research Note No. RN-2014-08A, 2014.

Van der Marel, Erik, and Ben Shepherd. “Services Trade, Regulation and Regional Integration: Evidence from Sectoral Data.” World Economy 36, no. 11 (2013): 1393 $-$ 1405.

Appendix

Table A.1 Regional trade agreements: member listing

Dummy	Members of the agreement
NAFTA	Canada, Mexico, United States
Europe	Austria, Belgium, Bulgaria, Cyprus, Czech Republic, Denmark, Estonia, Finland, France, Germany, Greece, Hungary, Ireland, Italy, Latvia, Lithuania, Luxembourg, Malta, Netherlands, Poland, Portugal, Romania, Slovakia, Slovenia, Spain, Sweden, United Kingdom
ASEAN	Brunei, Burma (Myanmar), Cambodia, Indonesia, Laos, Malaysia, Philippines, Singapore, Thailand, Vietnam
ANZCERTA	Australia, New Zealand

[1] This is model 2 in Fontagné, Guillin, and Mitaritonna (2011).

[2] Theory suggests an elasticity of 1, although it is often found to vary from that value. Based on past experience, we constrain this parameter to 0.8, but this choice does not affect the results.

[3] In the case of services under Mode 1 there are no transport costs and trade costs are simply the revealed protection exerted by the presence of regulation.

[4] Notice that τ equals 1 in absence of trade barriers.