ECONOMICS WORKING PAPER SERIES

FIRM HETEROGENEITY AND EXPORT PRICING IN INDIA

Michael A. Anderson
Martin H. Davies
José E. Signoret
Stephen L. S. Smith

Working Paper 2016-09-B

U.S. INTERNATIONAL TRADE COMMISSION
500 E Street SW
Washington, DC 20436

September 2016

We thank participants at the Spring 2015 Midwest International Economics Group, the 2014 Southern Economics Association meetings, especially Tom Prusa, and at the USITC Trade Seminar for helpful comments. We also thank Dylan Carlson, Chris Handy, Sommer Ireland, Richard Marmorstein, Daniel Molon, George Nurisso, Matthew Reardon, Daniel Rodriguez-Segura, Nathanael Snow, and Ricky Ubee for indefatigable research assistance.

Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research.

Firm Heterogeneity and Export Pricing in India
Michael A. Anderson, Martin H. Davies, José E. Signoret, and Stephen L. S. Smith
Office of Economics Working Paper 2016-09-B

September 2016

ABSTRACT

We examine the export pricing behavior of Indian manufacturing firms in the early 2000s using a unique data set that matches detailed firm characteristics with product and destination-level trade data. We find, in contrast to evidence for other countries, that firm productivity is negatively associated with export prices, and that export prices are negatively associated with distance, and positively associated with remoteness. We suggest that it is the higher cost of innovation in India, driving down the scope for quality differentiation, which leads to the negative association between productivity and prices. We use the framework of Antoniades (2015) to place our results (heterogeneous goods, homogeneous markets) relative to two other groups identified in the literature: (homogeneous goods, homogeneous markets) and (heterogeneous goods, heterogeneous market). To our knowledge this is the first empirical evidence consistent with this particular theoretical possibility.

Michael A. Anderson
Washington and Lee University

AndersonM@wlu.edu

Martin H. Davies
Washington and Lee University
Center for Applied Macroeconomic Analysis, Australian National University

DaviesM@wlu.edu

José E. Signoret
U.S. International Trade Commission

Jose.Signoret@usitc.gov

Stephen L. S. Smith
Hope College
slssmith@hope.edu

I. Introduction

Our paper contributes to the literature on firm heterogeneity and export pricing by analyzing the behavior of Indian manufacturing firms. We construct and exploit a new data set for India containing firm export transactions matched to firm characteristics to determine the sources of exporting success. This allows us to ask the question: in comparison to exporters in other countries examined thus far, do Indian firms behave differently?

We make two primary contributions. We are the first to examine the pricing behavior of Indian exporters. Second, we find a negative association between firm productivity and the prices firms charge in destination markets. This result, combined with a finding that prices are negatively associated with distance to destination market, and positively associated with remoteness, is in contrast to findings for exporters in other countries.

We contribute to a small, but burgeoning, literature which examines the pricing behavior of exporters in China (Manova and Zhang, 2012), the United States (Harrigan, Ma, and Shlychkov, 2015), and Europe (Portugal: Bastos and Silva, 2010; Hungary: Görg, Halpern, and Muraközy, 2010; France: Martin, 2012; and Colombia: Kugler and Verhoogen, 2012). These papers all find similar results, namely that more productive firms charge higher prices in export markets, and that prices increase with distance. Further, Manova and Zhang and Harrigan, et al. also find that prices fall with remoteness. These results suggest that more productive firms are quality upgrading.

Our results stand in contrast to this body of literature. We find that for Indian exporters, more productive firms charge lower prices, and that prices fall with distance and rise with remoteness. Further, these results are robust across industries.

While different from those for other exporting countries studied, our results are consistent with recent heterogeneous firm models that incorporate endogenous quality upgrading. Antoniades (2015) provides a framework which shows that the relationship between prices and productivity may be positive or negative depending on whether the scope for quality differentiation is high or low. The scope for quality differentiation, which reflects a firm’s ability to recover the innovation cost of quality upgrades, depends on market size, the degree of differentiation between varieties of goods, and the cost of innovation.

When the cost of innovation is high, firms producing heterogeneous goods will face a lower scope for quality differentiation (quality ladders are shorter),[1] in which case quality upgrades for more productive firms become smaller and the relationship between firm productivity and prices may be negative. As India is a developing country, Indian firms face a higher cost of innovation than firms in the developed countries noted above, and we suggest that our empirical results for India arise because quality ladders there are short (markets are homogeneous). China, also a developing and rapidly emerging economy, is commonly contrasted to India.[2] Relative to India, firms in China face larger markets and a lower cost of innovation, leading to a higher scope for quality differentiation and the observed positive relationship between productivity and price.

Based on the characteristics of goods (homogeneous or heterogeneous) and markets (homogeneous or heterogeneous), we divide the current empirical literature into two groups: (homogeneous goods, homogeneous markets) and (heterogeneous goods, heterogeneous markets). We place our result in a third group, (heterogeneous goods, homogeneous markets). To our knowledge we are the first to find empirically this result.

The paper proceeds as follows. Section II reviews the literature and Section III discusses the new data. Section IV presents our results in two parts: descriptive statistics on successful exporters’ pricing patterns and regression results that relate individual product price decisions to firm and destination market characteristics. Section V discusses our results and Section VI concludes.

II. Literature Review

The theoretical literature is instructive in highlighting the contrast in the behavior of Indian firms relative to the firms in other countries examined thus far. Melitz (2003) introduces firm level marginal cost heterogeneity into a model with beachhead costs and monopolistic competition. Because goods are homogeneous, firms compete only on price and, since mark-ups are constant, more productive firms charge lower prices. Since the lowest priced goods are the most competitive, prices are decreasing in the distance from the export market and increasing in remoteness.

These predictions run counter to the empirical studies mentioned above, which find a positive correlation between productivity and price. The common explanation is that firms in these countries compete both on quality and price. Baldwin and Harrigan (2011) modify Melitz (2003) to include a quality dimension. In their model, firms with higher unit costs produce higher quality goods and, because quality is increasing in cost at a sufficient rate, while they charge higher prices, their goods are more competitive because the price per unit of quality is less than for lower cost firms. This quality-adjusted heterogeneous-firms model predicts that export prices are increasing in distance and decreasing in remoteness, which fits the empirical evidence collected thus far.

The sample of firms we examine is drawn from a range of differentiated goods manufacturing sectors within which there are variations in quality. Antoniades (2015) provides a framework which helps illuminate the position of our result within the literature. His paper extends the model of Melitz and Ottaviano (2008), which includes a linear demand system in a model of monopolistic competition, to incorporate endogenous quality choice by firms. Lower cost firms choose higher quality and have higher mark-ups, which is a feature both of producing a variety of higher quality which increases demand and facing a lower elasticity of demand. Since marginal costs and mark-ups move in opposite directions, it is possible that the relationship between price and productivity may be positive or negative.

Whether it is positive or negative depends on the scope for quality differentiation, which in turn depends on the factors which influence a firm’s ability to recover the innovation costs of quality upgrading: on market size (L), the degree of differentiation between varieties (1/γ), and the cost of innovation (θ). The sign of this relationship depends on

$\frac{d p (c)}{d c} = \frac{1}{2} (1 - (β + δ) λ)$

where 1/c is productivity, β is a taste parameter which measures the appreciation of quality, δ measures the cost of upgrading quality, and λ is the scope for quality differentiation.[3]

When $λ < 1 / (β + δ)$ then the scope for quality differentiation is low and dp(c)/dc > 0, and prices and productivity are negatively correlated. When the scope for quality differentiation is high, or when quality ladders are long, then $λ > 1 / (β + δ)$ and the relationship between productivity and price is positive and prices are a good proxy for quality (Khandelwal, 2010). This is known as the heterogeneous markets case. There are two possibilities when the scope for differentiation is low ( $λ < 1 / (β + δ)$ ) and quality ladders are short, which is the alternative homogenous markets case. First, when goods are homogenous, firms find no purpose in quality upgrading and the relationship between prices and productivity is negative, as in Melitz and Ottaviano (2008). The alternative is when goods are heterogeneous and the scope for quality differentiation is low. Here firms will engage in quality upgrading, but while higher productivity firms choose higher quality and mark-ups are larger, they do not rise at a rate sufficient to offset their lower costs. Thus, more productive firms charge lower prices.

We now briefly summarize the empirical literature. Using 2005 Chinese firm and product data at the HS 8-digit level, Manova and Zhang (2012) find that successful exporters earn more revenue in part by charging higher unit prices and by exporting to more destinations than less successful exporters. Even within narrowly-defined product categories, firms charge higher unit prices to more distant, higher income, and less remote markets. Manova and Zhang argue that firms’ product quality is as important as production efficiency in determining these outcomes.^{^[4]} Harrigan, et al. (2015), using 2002 U.S. data at the HS 10-digit level, make a similar finding: U.S. firms charge higher prices for products shipped to larger, higher income markets, and to countries more distant than Canada and Mexico, a result they attribute to higher quality. Harrigan, et al. also find that firms’ ability to raise unit prices is positively affected by their productivity and the skill-intensity of production. On their face, the results relating to distance and number of markets appear consistent with the hypothesis first advanced by Alchian and Allen (1964), and developed by Hummels and Skiba (2004), that “per unit” transport costs raises relative demand for high quality goods (the “shipping the good apples out” hypothesis).

Bastos and Silva (2009) examine Portuguese firm-level data on exports by product and destination market. They find strong support that within-product unit values increase with distance; doubling distance increases unit values by nine percent (their distance elasticity is 0.05). Firm productivity is positively associated with firm prices; in addition they find that firm productivity “magnifies the positive effect of distance on within-product unit values,” which suggests that high-quality products from high-productivity firms are more successful in difficult markets. Likewise, Görg, et al. (2010), with Hungarian firm-level data on exports by product and destination market, find a substantial positive distance effect on unit values. They report distance elasticities consistently in the 0.08 $-$ 0.10 range; Hungarian export unit values are 25 $-$ 30 percent higher in the United States than in the EU. This effect holds most strongly for differentiated goods. They also report that unit values rise with firm productivity and with destination market income per capita, which they call “quality-to-market” effects.

Martin (2012) examines French exporting firms in 2003. Here again prices are positively associated with distance. The author finds that doubling distance increases prices by 3.5 percent (the elasticity of f.o.b. prices to distance is 0.05), an effect that is weakened for the Euro area subsample. The author attributes the latter point to incomplete exchange rate pass-through and the absence of country-specific tariffs for goods. The author also find evidence that the more differentiated is the good, the larger is the effect of distance on prices (a result obtained by interacting distance with the good’s elasticity of substitution).

Syverson (2007) investigates price dispersion in the ready-mix concrete industry in the United States. His model has heterogeneous firms (differing marginal costs) competing in a homogenous goods market with very high transport costs (so high that 348 markets consisting of contiguous counties are assumed to exist in the United States). The price data support the heterogeneous-firm model by showing a negative correlation between price dispersion, and upper-bound prices, and producer density. This stands in contrast to the predictions found in homogenous producer (with homogeneous goods) models.

Foster, Haltiwanger, and Syverson (2008) examine a small set of assumed homogenous goods manufacturers (of goods such as ice, concrete, sugar, boxes, oak flooring). Their data allows them to disentangle physical productivity (units of output) from revenue productivity, the latter being the measure typically used to measure firm efficiency. The authors find greater dispersion of physical productivity compared to revenue productivity; the former is negatively correlated with establishment-level prices while revenue productivity is positively associated with prices.

Using data from the Census of U.S. Manufactures over the period 1963 $-$ 1987, Roberts and Supina (1996, 2000) undertake two studies to examine how the patterns of prices and mark-ups vary with plant size. They choose products that are clearly homogeneous to remove other sources of heterogeneity. In Roberts and Supina (1996) they examine six homogeneous manufactured goods (white pan bread, coffee, tin cans, corrugated boxes, concrete, and gasoline). They find that output prices decline with plant size in five of six products (for gasoline there is no correlation), and that mark-ups decline in three and rise in two, with no relationship for gasoline. Roberts and Supina (2000) look at thirteen homogenous manufactured products and examine, in addition to the questions above, the persistence of prices over time, and find there is more persistence than would be generated by random movements. They also find that for all products, except gasoline and newsprint, large producers charge lower prices; that marginal costs are decreasing for most producers; and that mark-ups increase in six products, decrease in four, and have no relationship in two (gasoline and newsprint).

Using data from the Colombian manufacturing census, Kugler and Verhoogen (2012) find a positive correlation between both output and input prices and plant size; this positive correlation is also evident for export status. Using advertising and research and development (R&D) intensity as measures of the scope for quality differentiation they find a positive relationship between output prices and plant size, and input prices and plant size, which is stronger for sectors in which the scope for quality differentiation is higher. They match these empirical findings to a modification of the Melitz (2003) model which incorporates endogenous choice of output and input quality, which predicts the matching of more capable producers and higher quality inputs to produce higher quality outputs.

III. Data

Our detailed firm-level price, good, destination and firm characteristics dataset is assembled from several sources. We have detailed firm-level daily transactions data for Indian exporters in TIPS, a database collected by Indian Customs. TIPS contains detailed export data including the identity of the exporter, the date of transaction, the product type by 8-digit HS code, destination country, exit and destination port, and the quantity and the value of the export. We have useable data for four full fiscal years, 2000-2003, which cover the transactions at eleven major Indian seaports and airports.^{^[5]} For the purpose of our analysis we aggregate the data to fiscal-year average prices by firm.

The firm-product-destination data have quantity units attached. Wherever possible we “harmonize,” or standardize, the quantity units, adjusting the associated transaction value as required. For example, we convert metric tons and pounds to kilos, and we converted yards and feet into meters. For each product we keep only those observations in the “dominant” unit, the quantity unit with the largest share of that product’s exports.[6] This step is required as our model predicts prices (unit values) based upon firm and destination characteristics, and we cannot explain why a product has a certain price when measured in kilos, and why the price differs when measured in boxes.

It is possible that our quantity harmonization introduces selection bias into our sample if firms that ship in the dominant unit differ from the other firms in the sample. Alternatively the choice of unit may be related in some way to the destination country. By keeping only dominant units we reduce our sample from 27,403 to 21,385 observations, a 22 percent reduction, and the total value of exports in the sample falls by 8 percent.

To examine this possibility we run a probit where the binary dependent variable equals 1 if the firm-product-destination observation is measured in the dominant unit, 0 otherwise. We look for correlation with our vectors of firm and destination characteristics. Results are presented in Appendix Table A.1. We find one of two results across the variables: either a variable is statistically insignificant, suggesting that selection is not happening on that characteristic; or the marginal effect of the variable is small, suggesting that our sample does not suffer from severe selection bias. See the discussion in the Appendix for further details.

The TIPS data, once harmonized across quantity units, are matched with detailed firm-level data from Prowess, a proprietary database of Indian firm characteristics.^{^[7]} The dataset contains time series information back to 1989 on approximately 23,000 large- and medium-sized firms in India, and includes all companies traded on India’s major stock exchanges as well as other firms, including the central public sector enterprises. Its broad swath of Indian firms pay around 75 percent of all corporate taxes and over 95 percent of excise duties collected. From Prowess we derive information on employment, labor and capital use, expenses on intermediates, and other firm-level variables for manufacturing firms (our sector of interest). While Prowess contains information on overall foreign sales, it lacks information as to the products exported, their destination markets, and their export unit prices. Matching firms between TIPS and Prowess brings these additional dimensions.^{^[8]} The results in this paper are based on a matched dataset on 1,018 manufacturing firms.^{^[9]}

Finally, we use country characteristic data (income, population, and distance from India) from the publicly available CEPII Gravity database (Head, Mayer, and Ries, 2010).

We measure export prices as unit values: export revenue by product category divided by the number of units exported in that category. The TIPS data are reported at an HS 8-digit level of detail, though our data allows us to ultimately define a “product” at a much finer detail than that, a level we refer to as “HS 8-plus.”^{^[10]} At this fine level of differentiation, the rich detail of the TIPS side of our merged data allows us to distinguish a firm’s patterns of prices for an identical good across different destination countries.

Tables 1 and 2 offer an initial view of the export behavior of the firms in our working sample. The picture that emerges is a familiar one, though with some differences from the United States. The most successful firms in export value terms dominate the export sector in many dimensions. The top ten percent of the firms account for approximately 80 percent of exports by value (Table 1). This is less concentrated than the behavior of U.S. exporters in 2000, for which the top ten percent account for 95 percent of the value of all exports.

Table 1. Distribution of Export Values by Firm, Percent Shares

Year	Top 1 percent	Top 5 percent	Top 10 percent	Top 20 percent	Bottom 80 percent
2000	32.1	60.1	73.6	87.7	12.3
2001	44.4	68.9	79.5	89.1	10.9
2002	43.6	67.6	79.7	89.1	10.9
2003	40.6	70.1	83.3	93.5	6.5

Source: Authors’ calculations from estimating sample

A small group of successful exporters sell far more products per firm, and to far more destinations per firm, than do other exporters (Table 2): 13.5 percent of our sample sold 10 or more goods to 10 or more destinations in 2003. The modal Indian firm in our sample exports between 2 and 5 products to between 2 and 5 markets (21.2 percent of all firms). If one considers the proportion of firms that export to one market only, the figure in our sample is 26 percent versus 65 percent for the United States in 2000.^{^[11]}

Table 2. Cross-Tabulation of Firm Export Destinations and Product Diversification, 2003

Percent of firms	1 Destination	2-5 Destinations	6-10 Destinations	>10 Destinations	Total
1 Product	17.8	3.4	3.0	0.2	21.7
2-5 Products	6.7	21.2	3.3	0.7	31.7
6-10 Products	0.8	9.0	6.8	2.6	19.2
>10 Products	0.7	4.9	8.2	13.5	27.2
Total	25.9	38.6	18.6	16.9	100.0

Source: Authors’ calculations from estimating sample.
Note: Products are defined at HS 8-plus level discussed in text.

IV. Results

We offer two sets of results. The first consists of descriptive findings about Indian exporters’ pricing behavior. The evidence here suggests that Indian firms may be increasing export revenue through quantity increases rather than through price increases. In the second set of results, we estimate the relation between prices and destination market characteristics and firm characteristics. We are particularly interested in the relationship between firm productivity and export prices, and our finding is that firm productivity is associated with lower prices, a result that stands in contrast to other results in the literature.

IV.A. Indian Export Price Patterns

Between 2000 and 2003 Indian export revenue (in our sample) grew by a factor of more than 3.5. Remarkably, for products and markets with continuing sales, revenue increases were achieved by rising volumes in the face of falling prices.

Individual exporters’ overall revenue changes are the net effect of revenue changes on their intensive and extensive margins. Price and quantity changes on shipments to existing markets (continuing goods and destinations) generate “intensive margin” changes, while revenues from new markets (new goods and destinations) constitute the extensive margin.

We adopt a simple approach to assess the price and quantity components of revenue growth on the intensive margin combined with a broad definition of the intensive margin.^{^[12]} We calculate, at the firm-product level, the weighted annual rates of change in price and quantity over all the continuing destination markets to which the given firm exports the given product, using destination market revenue as weights.

We restrict ourselves to firm-product-destination combinations that can be thought of as plausibly “continuing.” So, for instance, when a firm exports a product to a given set of destination markets in consecutive years, the destination-weighted rates of price, quantity and revenue change can be calculated. Further, we include all such observations with one- or two-year gaps (two years being the maximum possible gap in our four-year sample). For example, a firm that exports a particular good to a given destination only in 2000 and 2003 is considered to be “continuing.” In an environment with high exit rates, these continuing firm-product-destination combinations represent the behavior of some of India’s most successful exporters. In our sample, 48 percent of total export revenue comes from continuing exports defined in this fashion. The remaining 52 percent of export revenues come from shipments which represent one-time sales by a firm of a given product to a given destination (at least in our sample).

We adopt a simple decomposition, as follows, where f, p, and d (d = 1, 2, …D) subscript firms, products and destination markets (and D is the total number of a firm’s destinations for any given product p). Define P_fpd and Q_fpd to be the unit value and quantity of firm f’s shipment of product p to destination d. Suppressing time subscripts, in any given year the firm’s revenue from exporting a product, Y_fp, is the sum of revenue earned across all D destinations:

$Y_{f p} = \sum_{d = 1}^{D} P_{f p d} Q_{f p d}$ (1)

Taking the total differential of Y_fp with respect to P_fpd and Q_fpd, and defining $θ_{f p d}$ to be the firm’s product p revenue share attributable to sales in destination d, we can decompose intensive margin export revenue growth for product p ( ${\hat{Y}}_{f p}^{I M}$ ) into the (destination-weighted average) contributions of price and quantity changes across destinations:

${\hat{Y}}_{f p}^{I M} = \sum_{d = 1}^{D} θ_{f p d} {\hat{P}}_{f p d} + \sum_{d = 1}^{D} θ_{f p d} {\hat{Q}}_{f p d}$ (2)

${\hat{P}}_{f p d}$ and ${\hat{Q}}_{f p d}$ represent the rate of change in unit value and quantity, for destination d. The revenue-weighted averages, across destinations, of price and quantity changes give us the intensive margin’s price change ( $\sum_{d = 1}^{D} θ_{f p d} {\hat{P}}_{f p d})$ and quantity change ( $\sum_{d = 1}^{D} θ_{f p d} {\hat{Q}}_{f p d}$ ) for each firm-product (f-p) observation. (For observations with gaps between appearances, we calculate price, quantity and revenue rates of change over the entire period and attribute that change to the final year.) All calculations are made at the HS 8-plus level. Note that each f-p observation with continuing destinations allows calculation of price- and quantity-change observations as long as there is a previous year of data, regardless of the number of destinations to which the firm ships the product.

Results are summarized in Table 3.[13] There are 1,419 unique firm-product-year observations over fiscal years 2001-2003 (keeping in mind that 2000 is dropped in calculating the rates of change). The table reports medians of the price, quantity and revenue variables calculated for each observation. Revenue changes appear to be dominated by quantity changes (line 1). The median firm-product annual revenue change was 4.1 percent, while the median price change was -1.1 percent and the median quantity change was 12.1 percent. When we restrict the sample to firm-product observations with positive revenue change only (line 2), the median annual revenue change rises to 154.0 percent, while the median price change is 0.1 percent (and of quantity, 151.5 percent). Clearly, many “successful” exporters $—$ those with revenue increases $—$ gained those revenue increases by large quantity increases in the face of flat or falling unit prices.

Table 3. Median Destination-Weighted Price, Quantity and Revenue Changes, 2001-2003

All Continuing Firm-Product Observations	%Δ Price	%Δ Quantity	%Δ Revenue

All Continuing Firm-Product Observations (n = 1,419)	-1.1	12.1	4.1

All Continuing Firm-Product Observations with Positive Revenue Growth (n = 726)	0.1	151.5	154.0

Source: Authors’ calculations from estimating sample.
Note: Products defined at HS 8-plus, using all continuing firm-product observations as defined in text. Figures presented are the medians by variable.

Cross-tabulations of the price and quantity changes (Table 4) confirm this: 49.0 percent of firm-product observations with positive revenue growth experienced lower prices (that is, 356 out of 726 firm-product combinations). Clearly, Indian exporters, at least in this period, experienced price decreases in their shipments as measured at a HS 8-plus level.[14]

Table 4.Cross-Tabulation of Destination-Weighted Price and Quantity Changes,

For all Continuing Firm-Product Observations

4A. All Continuing Firm-Product Observations (n = 1,419)
Percent (number)	%Δ Quantity≤ 0	%Δ Quantity> 0	Total
%Δ Price ≤ 0	20.7 (295)	33.3 (472)	54.1 (767)
%Δ Price >0	23.0 (326)	23.0 (326)	45.9 (652)
Total	43.8 (621)	56.2 (798)	100.0 (1,419)

4B. Continuing Firm-Product Observations With Positive Revenue Growth (n = 726)
Percent (number)	%Δ Quantity≤ 0	%Δ Quantity>0	Total
%Δ Price ≤ 0	0.0 (0)	49.0 (356)	49.0 (356)
%Δ Price >0	7.6 (55)	43.4 (315)	51.0 (370)
Total	7.6 (55)	92.4 (671)	100.0 (726)

IV.B. Controlling for Destination Market and Firm Characteristics

We now examine how firm prices are associated with a range of firm and destination characteristics. Firm characteristics include the capital to labor ratio, labor usage (which we take as a proxy for size), and total factor productivity (TFP);^{^[15]} destination-market characteristics consist of distance, remoteness, GDP, and GDP per capita.[16]

As in Harrigan, et al. (2015), we consider the possibility of selection bias because firm prices are only observed if firms choose to export to particular destinations, and we implement their three-stage estimator, itself an extension of Wooldridge (1995). The first stage is a Probit of entry (of a firm in a particular destination in a particular year) on all exogenous export-market characteristics (X_d), firm characteristics (X_f), and a year-specific intercept $α$ . Omitting time subscripts we have:

$\Pr (Y_{f p d} > 0) = Φ (α + δ_{1} X_{d} + δ_{2} X_{f})$ (3)

Equation (3) is estimated over an expanded sample of all possible firm-destination-year combinations; that is, it is applied to a “rectangularized” data set with zeros added. The inverse Mills ratio ${\hat{λ}}_{f p d}$ is then included in the second stage which explains observed (i.e., positive) firm-product-destination revenue based upon export-market and firm characteristics and product fixed effects ( $α_{p}$ ):

$\ln Y_{f p d} = α_{p} + ζ_{1} X_{d} + ζ_{2} X_{f} + γ \hat{λ}_{f p d} + u_{f p d}$ (4)

Quasi-residuals, formed as the actuals residuals plus the estimate term for the inverse Mills ratio, ${\hat{η}}_{f p d} = {\hat{u}}_{f p d} + γ {\hat{λ}}_{f p d}$ , from this second stage are then entered as a selection control in the price regression:

$\ln P_{f p d} = α_{p} + β_{1} X_{d} + β_{2} X_{f} + ψ {\hat{η}}_{f p d} + ϵ_{f p d}$ (5)

This approach is more flexible than the two-step Tobit approach proposed by Wooldridge (1995) in that the estimated effects on entry, the $δ$ ’s in equation (3), are allowed to differ from the effects on export intensity, the $ζ$ ’s in equation (4).^{^[17]} While the rich data used in Harrigan, et al. (2015), allows them to estimate regressions (3) and (4) product by product, the limited number of firms in our sample makes this approach unpractical, since in many instances it would entail estimation with very few data points. Thus, we initially estimate these regressions over the whole sample and then relax this treatment by conducting the analysis by subsamples based on broad industries (e.g., textiles and textile articles).

Descriptive statistics on the estimating sample are presented in Table 5, and regression results are presented in Table 6. The dependent variable in every case is the unit value of a firm’s exports at the product-destination-year level, and all regressions use product fixed effects and destination standard-error clusters. Note that compared to the previous descriptive analysis we have many more observations because the data are in levels (not rates of change) and are not aggregated across destinations.

Table 5A. Descriptive Statistics from Estimating Sample (Table 6, Column 1), in levels,

n = 20,850

Variable names	Mean	Std. Dev.	Min	Max
price (USD)	1,005	19,689	0.0000004	2,299,543
gdppc (USD)	13,573	12,299	86	50,987
gdp (USD millions)	1,291,664	2,805,356	147	10,400,000
dist (km)	5,928	3,586	683	16,937
remote	0.00015	0.00009	0.00003	0.00037
tfp	126	85	22	444
klabor (USD thousands)	14	20	0.27	338
labor (USD thousands)	211	449	0.10	10,997

Table 5B. Descriptive Statistics from Estimating Sample (Table 6, Column 1), in logs,

n = 20,850

Variable names	Mean	Std. Dev.	Min	Max
price (USD)	1.65	3.04	-16.98	14.65
gdppc (USD)	8.66	1.63	4.45	10.84
gdp (USD millions)	11.96	2.23	4.99	16.16
dist (km)	8.51	0.61	6.53	9.74
remote	-8.99	0.70	-10.44	-7.90
tfp	4.64	0.63	3.10	6.10
klabor (USD thousands)	2.16	0.90	-1.31	5.82
labor (USD thousands)	4.23	1.57	-2.30	9.31

Table 6A. Firm-Product Pricing by Destination and Firm Characteristics $—$ For All Goods $-$ Log price

Variables	(1)	(2)
loggdppc	0.0892***	0.177***
	(0.0209)	(0.0277)
loggdp	0.0366***	0.271***
	(0.0133)	(0.0540)
logdist	-0.0242	-0.373***
	(0.0473)	(0.0661)
logremote^†	0.00446	0.361***
	(0.0432)	(0.0779)
logtfp	-0.171**	-0.162**
	(0.0827)	(0.0816)
logklabor	0.0823	0.0933*
	(0.0554)	(0.0560)
loglabor	0.0645*	0.181***
	(0.0345)	(0.0334)
selection^††		0.211***
		(0.0464)
Observations	20,850	20,850
R-squared	0.862	0.871
Fixed effects	Prod	Prod
SE clusters	Country	Country

Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1). Pooled annual data for fiscal years 2000-2003. All regressions include year fixed effects. Note that the observation count for the entire sample slightly exceeds the sum of the observations for the three sub-samples, as outlier trims for the sub-samples are done individually versus over the entire sample.
†Remoteness definition as described in the Appendix.
††Selection procedure as described in text.

Table 6B. Firm-Product Pricing by Destination and Firm Characteristics $—$ Textiles and Textile Articles $-$ Log price

Variables	(1)	(2)
loggdppc	0.0326	0.127***
	(0.0216)	(0.0249)
loggdp	0.0135	0.189***
	(0.0126)	(0.0387)
logdist	0.105**	-0.162**
	(0.0440)	(0.0678)
logremote^†	0.0344	0.240***
	(0.0384)	(0.0510)
logtfp	-0.123*	-0.137**
	(0.0670)	(0.0688)
logklabor	0.00903	0.0102
	(0.0311)	(0.0308)
loglabor	0.0965***	0.162***
	(0.0226)	(0.0269)
selection^††		0.0355***
		(0.00698)
Observations	2,915	2,915
R-squared	0.917	0.919
Fixed effects	Prod	Prod
SE clusters	Country	Country

Table 6C. Firm-Product Pricing by Destination and Firm Characteristics $—$ Machinery, Appliances and Electrical Equipment $-$ Log price

Variables	(1)	(2)
loggdppc	-0.0765	0.0136
	(0.0499)	(0.0472)
loggdp	-0.0153	0.194***
	(0.0401)	(0.0555)
logdist	0.0330	-0.330***
	(0.105)	(0.112)
logremote^†	0.00256	0.347***
	(0.117)	(0.126)
logtfp	-0.570***	-0.565***
	(0.193)	(0.173)
logklabor	0.106	0.0258
	(0.194)	(0.183)
loglabor	0.309***	0.388***
	(0.116)	(0.105)
selection^††		0.269***
		(0.0386)
Observations	4,233	4,233
R-squared	0.904	0.913
Fixed effects	Prod	Prod
SE clusters	Country	Country

Table 6D. Firm-Product Pricing by Destination and Firm Characteristics $—$ All Other HS Chapters $-$ Log price

Variables	(1)	(2)
loggdppc	0.106***	0.163***
	(0.0221)	(0.0274)
loggdp	0.0514***	0.230***
	(0.0167)	(0.0449)
logdist	-0.0471	-0.300***
	(0.0519)	(0.0586)
logremote^†	-0.0319	0.244***
	(0.0561)	(0.0701)
logtfp	-0.214**	-0.208**
	(0.0869)	(0.0881)
logklabor	0.126*	0.158**
	(0.0717)	(0.0754)
loglabor	0.0161	0.0973**
	(0.0466)	(0.0394)
selection^††		0.242***
		(0.0567)
Observations	13,657	13,657
R-squared	0.829	0.842
Fixed effects	Prod	Prod
SE clusters	Country	Country

†Remoteness definition as described in the Appendix.
††Selection procedure as described in text.
Robust standard errors in parentheses (*** p<0.01, ** p<0.05, * p<0.1). Pooled annual data for fiscal years 2000-2003. All regressions include year fixed effects. Note that the observation count for the entire sample slightly exceeds the sum of the observations for the three sub-samples, as outlier trims for the sub-samples are done individually versus over the entire sample.

Column (1) is a regression on all firm-product-destination observations in our sample, with no selection correction. Column (2) presents the results for the same sample as column (1) with the three-stage selection correction.^{^[18]} Subsequent columns present results for products in particular 2-digit HS chapters: textiles and textile articles (columns 3 and 4); machinery, appliances and electrical equipment (columns 5 and 6); and the rest of the two-digit HS chapters (columns 7 and 8). For each break-out the first column shows the uncorrected results; the second column shows the results with the selection correction.

These results are drawn from a sample that has been trimmed based upon the 5^th and 95^th percentiles of the distribution of the TFP variable. This variable has some extreme values, possibly related to data reporting errors for the firms in the sample. We observe the outliers for firms in particular years, and not typically by firms across all four years, which increases our doubts about the validity of the outliers. In results not reported here we estimated our equation across two other trim thresholds (90/10, 80/20) and on the entire sample. The results are robust to the various trims, with the exception that TFP is no longer significant in the entire sample.

Column (2) is our baseline regression on all firm-product-destination observations with a selection correction. We find a positive association between unit values and destination GDP, GDP per capita, and remoteness. The capital to labor ratio and our measure of labor size both have positive and significant coefficients. Overall our model performs well; R-squared values are about 87 percent.

In contrast to the literature we find a negative association between TFP and export prices; more productive firms on average charge lower prices. We also find, in contrast to the literature, a negative association between distance and prices, and a positive association between remoteness and prices.

In subsequent columns we examine the same model of firm prices applied to particular 2-digit HS chapters. In this discussion we focus only on the result with the sample correction (columns 4, 6, and 8). Across the three breakouts our results are similar, both firm TFP and distance have a negative association with prices, and remoteness bears a positive coefficient.^{^[19]}

Consider the TFP variable. The coefficient ranges from -0.14 to -0.21 in three of the four regressions (and is -0.57 for the machinery category). At -0.16 it suggests firms with a ten percent higher productivity than other firms, all else equal, charge about 2 percent lower prices. A firm that raises its productivity by one standard deviation above the mean of all firms would be predicted to reduce prices by about 11 percent.[20] We note that our negative coefficient on productivity is robust to how this variable is measured. When we use value-added per worker as a measure of firm productivity we again obtain a consistently negative (and statistically significant) association with firm prices.^{^[21]}

IV.C. Robustness Checks

We perform several robustness checks. To examine stability of coefficient estimates we reestimate the sample-corrected results (Table 6 column 2) this time with either only the firm variables, or only the destination variables. Also, we reestimate Table 6 column 2 using only those firms that, over the 4 year time period, export to more than one destination. This provides a robustness check on the coefficients on the destination variables; it could be argued that these coefficients should be determined only with firms that export to multiple destinations. The results are found in Table 7.

Table 7. Robustness Checks, log price as the dependent variable

Variables	(1)	(2)	(3)
loggdppc	0.170***		0.168***
	(0.0272)		(0.0282)
loggdp	0.248***		0.254***
	(0.0528)		(0.0513)
logdist	-0.341***		-0.348***
	(0.0659)		(0.0645)
logremote	0.334***		0.332***
	(0.0748)		(0.0755)
logtfp		-0.185**	-0.149*
		(0.0884)	(0.0880)
logklabor		0.0961	0.0935
		(0.0594)	(0.0638)
loglabor		0.0895***	0.183***
		(0.0323)	(0.0342)
selection	0.193***	0.0769**	0.208***
	(0.0454)	(0.0308)	(0.0469)
Observations	20,850	20,850	20,265
R-squared	0.869	0.862	0.871
Fixed effects	Prod	Prod	Prod
SE clusters	Country	Country	Country

Robust standard errors in parentheses,
Selection corrections use firm and destination variables
*** p<0.01, ** p<0.05, * p<0.1

Columns 1 and 2 report respectively the destination-variables-only and firm-variables-only regressions. Both panels of results are broadly comparable to the main results (Table 6 column (2)) where both destination and firm variables are both included. The exception (column 2) is that the capital-labor ratio is no longer statistically significant. When we reestimate our model using only those firms that export to more than one destination (column 3) the results are very similar to those from the entire sample. The coefficients on both the destination and the firm variables are little changed.

V. Discussion

As noted in the literature review, there are three cases to consider distinguished first by whether goods are heterogeneous or homogenous, and then for the heterogeneous goods case, by whether the scope for quality differentiation is high or low, and thus whether markets are heterogeneous or homogeneous. We present these three cases in Figure 1, which is drawn holding market size constant. Zone I is the homogeneous goods case for which the correlation between prices and productivity is negative. Since firms producing homogeneous goods are unconcerned with quality, whether the cost of innovation is high or low is irrelevant. Firm-level studies which align with zone I, which is classified as (homogeneous goods, homogeneous markets), are Roberts and Supina (1996, 2000), Syverson (2007), and Foster, et al. (2008). In zone III goods are heterogeneous and the cost of innovation is low. This leads to heterogeneous markets (or long quality ladders) and prices are a good proxy for quality. Bastos and Silva (2010), Görg, et al. (2010), Kugler and Verhoogen (2012), Manova and Zhang (2012), Martin (2012), and Harrigan, et al.(2015) are all placed in zone III, which is classified as (heterogeneous goods, heterogeneous markets). Finally zone II, classified as (heterogeneous goods, homogeneous markets), is the case where goods are heterogeneous and the cost of innovation is high. In this zone, the correlation between prices and productivity is negative and, although goods are heterogeneous, this is classified as homogeneous markets because of the negative correlation. Our findings suggest that, on average, Indian manufacturing firms belong in this zone. The upward sloping boundary between zones II and III is the boundary between the scope for quality differentiation being low (zone II) or high (zone III). Along the boundary, the scope for quality differentiation is constant, and thus as the degree of differentiation between goods increases, the cost of innovation must also increase.

Figure 1: Placement of Empirical Results

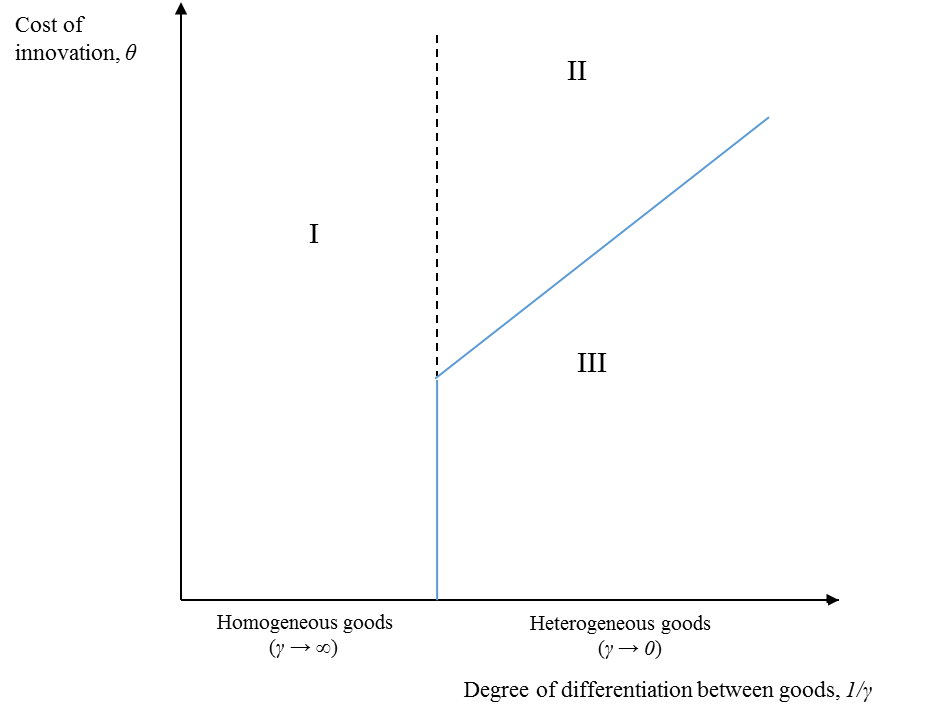
This figure illustrates the potential outcomes based on the
cost of innovation and the degree of differentiation between goods

Zones

I. (Homogeneous goods, homogeneous markets): Roberts and Supina (1996, 2000); Syverson (2007); Foster, et al. (2008)

II. (Heterogeneous goods, homogeneous markets): this paper.

III. (Heterogeneous goods, heterogeneous markets): Bastos and Silva (2010); Görg, et al. (2010); Kugler and Verhoogen (2012); Manova and Zhang (2012); Martin (2012); Harrigan, et al. (2015).

There is clear evidence that the cost of innovation is lower in developed relative to developing countries (Trefler, 1993; Hall and Jones, 1999; Harrigan, 1999; Acemoglu and Zilibotti, 2001). As noted by Antoniades (2015), in less developed countries where the cost of innovation is higher, the scope for quality differentiation is lower, and the correlation between prices and productivity may become negative. We argue that the cost of innovation is the key factor driving the difference in export pricing behavior between firms in the developed countries noted above relative to India. A more detailed comparison between China and India is necessary given the similarity of these countries in terms of development and the observed opposing signs between these countries in the relationship between export prices and productivity.

To begin, we note that we are examining the countries over roughly the same time period (2000 $-$ 2003 for India against 2003 $-$ 2005 for China, which is the range of Manova and Zhang’s, 2012, sample). Since we are concerned with the scope of quality differentiation, we compare the countries on market size and cost of innovation. There is no way to make judgements about whether the sample of goods examined in one country is more or less differentiated than that for the other.

Over this period, Chinese firms faced larger markets, both at the domestic and global levels. The Chinese domestic market was larger (a larger populace with higher income) and less segmented than in India, which has a large number of different language groups and a poorer transport infrastructure. China began to follow a strategy of export-led growth in the late 1970s, and as a result Chinese firms in the early 2000s had an awareness of, and were more fully equipped to exploit, export opportunities in the global market. On the other hand, Indian firms were less exported oriented. As evidence, in 2003, merchandise exports in China were 26.6 percent of GDP and 9.3 percent in India.[22] This was, in part, because the impediments to exporting were high. For example, Roy (2002) found than an India exporter had to obtain 258 signatures and make 119 copies in order to export a product.[23]

Since the late 1960s, India had in place policies which restricted the scale of enterprises, preventing in particular the development of large scale labor-intensive manufacturing. This began to be dismantled in the late 1990s, however it was still partially in place in 2007. Further, labor laws were (and continue to be) highly restrictive: for firms of over 100 workers it was almost impossible to fire workers, or to reassign them from one task to another. It was (and still is) difficult to close an ailing firm, with a highly inefficient set of bankruptcy procedures taking, on average, 10 years to complete (Panagariya, 2008, p. 294). Goldberg, Khandelwal, Pavcnik, and Topalova (2010a) find that product churn is low amongst Indian firms, with adjustments of product mix in multi-product firms limited almost entirely to product additions, without the shedding of existing products. They suggest that, given the restrictions mentioned above, it is difficult for firms to adjust their product mix to more efficiently allocate resources, leading to a lack of creative destruction along product lines. Dougherty (2007) also notes that regulations in India impede both the expansion of successful firms and the closing of unsuccessful ones.

The restrictions on scale and the difficulty of deploying, or redeploying, resources towards, or away from, innovative activity are evidence of costly hurdles that firms must overcome and which add to the cost of innovation.[24] Finally, China had a relative, and absolute, abundance of human capital, a key input into R&D, as evidenced by the secondary school enrolment rate in China in 2003 at 60 per cent, versus 51 percent for India, or the literacy rate (90 percent China in 2000 versus 61 percent in India in 2001).[25]

While there is no direct data on the cost of innovation in China and India during this period there is information on R&D activity in each country, which we use to make an inference about the ability of each country to undertake innovative activity. From two separate sources we compare R&D expenditure in manufacturing as a share of manufacturing output in China relative to India over the years 2008 $-$ 2010. We find that China’s share is 7.5 times that of India.[26] Using World Bank KAM data Dahlman (2007) finds that in 2004 the number of R&D researchers per million of population is six times larger in China than India (708 to 119). In the same year the proportion of GDP spent on R&D in China was 1.44 in comparison to 0.85 in India, and royalty and license fee payments per million of population were 10 times higher in China. Finally using phones (fixed or mobile) and internet usage, both per unit population, as a proxy measures for the level of the information technology infrastructure, a key input into innovative activity, the level in China was nearly 6 times that in India in 2004 for phones, and more than double for internet usage.

To determine what is driving our results, and to make the case that more productive firms producing heterogeneous goods are charging lower prices, we divide our sample along two lines. Firstly by the ternary Rauch categories (homogeneous, reference-priced, and differentiated), and secondly into the industry groups described in Table 6. We make this second distinction because the majority of our observations fall into the former two categories (textiles and textile articles at 14.0 percent; and machinery, appliances, and electrical equipment at 20.3 percent). We compare our results, examining both the unconditioned and conditioned correlations, with others in the literature, and in particular Kugler and Verhoogen (2012) and Manova and Zhang (2012).

Following Sutton (1998), Kugler and Verhoogen (2012) use R&D and advertising intensity as a measure of the scope for quality differentiation. They find that the correlation between prices and firm size is increasing in the scope for quality differentiation. Similarly, using Rauch categories to measure the scope for quality differentiation, Manova and Zhang (2012) find that the correlation between firm export prices and export sales increases as the scope for quality differentiation increases. Using Rauch categories, we find that the correlation between prices and firm size, proxied by either by firm’s total sales or labor force, is negative for homogeneous goods and positive for reference-priced and differentiated goods (see the estimated coefficients in Table 8).

Table 8. Correlation of Export Price with Firm Size

8A. Measuring size by sales: independent variable = ln(Sales)
Type of good	Coefficient (1)	SE (2)	t (3)	P-val (4)
Differentiated	0.168	0.019	8.78	0.000
Reference priced	0.289	0.022	13.06	0.000
Organized exchange	-0.106	0.033	-3.23	0.001
Reference priced and organized exchange	0.239	0.02	12.06	0.000

8B. Measuring size by labor force: independent variable = ln(Labor)
Type of good	Coefficient (1)	SE (2)	t (3)	P-val (4)
Differentiated	0.218	0.018	11.95	0.000
Reference priced	0.337	0.019	17.66	0.000
Organized exchange	-0.060	0.031	-1.93	0.054
Reference priced and organized exchange	0.286	0.017	16.56	0.000

Since we have measures of firm productivity, in contrast to Kugler and Verhoogen (2012) and Manova and Zhang (2012), we can examine the correlations between export prices and productivity. Dividing our sample into industry groups, we find that the correlation between prices and productivity in the “machinery” group, where goods are exclusively differentiated according to the Rauch categorization, is significant and strongly negative (Table 6).^{^[27]}

The empirical evidence suggests that the finding of a negative correlation between productivity and export prices in our sample is not driven by firms producing homogenous goods. Hence, although our result is classified as homogeneous markets because of the negative correlation between prices and productivity, the firms in our sample are in the majority producing heterogeneous goods. Further, our result is, if anything, strongest (most negative) for firms in the “machinery” group in which all goods are classified as differentiated. Given both that these goods are clearly heterogeneous, and the findings of the papers located in zone III, this is where one might expect the correlation to be most positive relative to the two other groups. Our interpretation is that our results belong in zone II, where goods are heterogeneous and the scope for quality differentiation is low. While Antoniades (2015) points to the theoretical possibility of this relationship, to our knowledge we are the first to find evidence consistent with this result.

Finally we provide a discussion of the relationship between export prices and distance and remoteness. In Harrigan, et al. (2015) and Manova and Zhang (2012), prices rise with distance and fall with remoteness. We find that prices fall with distance and rise with remoteness. These differences reflect the relationship between prices and quality: whether it is increasing (prices are a good proxy for quality, quality ladders are steep) as in Harrigan, et al. and Manova and Zhang, or decreasing (quality ladders are short), as in this paper. When firms compete on both price and quality, the most competitive goods are the ones with the lowest prices per unit of quality. For the United States and China these goods are the ones with the highest prices, and for India the lowest prices. Hence, the Indian goods that make it to the most distant or competitive (least remote) markets have the lowest prices.

VI. Conclusion

Using a unique dataset, we are the first to examine the pricing behavior of Indian exporters. Our empirical findings show a negative correlation between export prices and productivity, as well as export prices and distance, and a positive correlation between export prices and remoteness. The heterogeneous firms and export pricing literature, thus far, finds the opposite sign for each of these relationships.

The theoretical framework of Antoniades (2015) is useful in positioning our result, which is classified as (heterogeneous goods, homogeneous markets) relative to two other identified groups: (homogeneous goods, homogeneous markets) and (heterogeneous goods, heterogeneous markets). To our knowledge this is the first empirical evidence consistent with this particular theoretical possibility.

We suggest that because Indian firms face a higher cost of innovation, the scope for quality differentiation is low (quality ladders are short). Further, we suggest that while Indian firms engage in quality upgrading, the markups of higher-productivity firms are not large enough to offset their lower marginal costs. As a result, prices fall as productivity rises.

Appendix: Data

1. Data construction and “HS 8-plus” level of product detail.

Our main analysis relies on a merged dataset built by a firm-by-firm match of TIPS and Prowess data. TIPS data required considerable preparation for this merge, over and above simply aggregating its daily data to a fiscal year basis.

Consider firm names, which are recorded by hand at the point of collection (ports) with occasional spelling errors and frequent variants. We use two fuzzy-logic routines, Levenshtein distance and bigram comparisons, to match firm names in the sample. Some matches were done “by hand” based upon values in the fuzzy-logic comparisons. Wholesalers are excluded for the sake of focusing on the trading behavior of production firms, which requires several data-filtering criteria. If the firm name contains “Exporter,” “Importer,” or other key words it is removed from the sample.^{^[28]} In addition, we exclude firms that export goods in more than nine two-digit HS chapters.

Although the TIPS data are reported at the 8-digit HS level, we use the firm’s own product labels to obtain the actual product lines used in this study. For example, to take a non-manufacturing example, instead of looking at the unit value of 8-digit HS code 09101020 that includes a variety of spices, we are able to use the product labels to obtain the unit value, or price, of “curry powder” and “ginger” and other similar fine-grained prices. The result is something much more detailed than 8-digit data.^{^[29]} When this process is complete the mean number of individual product lines in an HS category is 11, with a median of 3. We refer to this level of disaggregated data as HS 8-plus.

Finally, inside of an HS8 or HS 8-plus code the quantity units can vary widely. This matters. The dependent variable in our empirical work is the export product price, defined as an export unit value and calculated as the relevant total value of exports divided by quantity. So, for instance, a firm’s average price for selling a particular product to the United States in any given year would be the value of sales divided by, say, the metric tons sold. But in many of the single firm-product-destination categories, export values are reported in several different units, such as “buckles,” kilos, pounds and “boxes,” the sum of which yields the total value of exports for that firm-product-destination observation.

We choose to aggregate and “harmonize” these values where there are well-established conversion factors for the units. Therefore we convert pounds to kilos, and tons to metric tons, and so on, prior to calculating unit values. However, there remain thousands of lines of data where the conversion factors are unknown, or for which the reporting of separate lines based on different quantity measures strongly suggests that there are in fact underlying differences between the goods reported in those lines (even when they are in the same 8-digit HS category). It is not possible to make meaningful unit value comparisons, or aggregations, across different units in these instances. (Is a good sold to France at $2 per buckle earning a higher price than that same 8-digit HS good sold to France at $350 per ton?) Accordingly, for the analysis reported here we keep only the dominant unit in each HS line, by value, and drop the others.

As noted in the text, our approach here has the potential to introduce selection bias into our regression results. Firms that export in the dominant unit may differ from those who export in other units. Alternatively, it may be the case that destinations that receive goods in the dominant unit differ from those that receive exports in other units. In Table A.1 we report the results of a linear-probability model and a probit model where in each case where the binary dependent variable equals 1 when the firm-product-destination observation is in the dominant unit, and 0 when it is in another unit. The regressions include product fixed effects. A large majority of observations are in the dominant unit; in the linear-probability model 78 percent of the observations are 1’s.

Across the two models most of the firm and destination variables are statistically insignificant. The exceptions are distance, TFP, and labor (the wage bill, a measure of firm size). For these three variables the marginal effect of a standard deviation increase in the variable, with other variables at means, is quite small. The largest clinical effect is for loglabor in the linear-probability models, where a one-standard deviation change is predicted to change the probability of moving from a 0 to a 1 by 2.61 percent, a small change. A complete table of clinical effects is available from the authors.[30]

Merging the TIPS and Prowess databases presents further technical problems in matching firm names. But after this merge and a final merge with CEPII destination market characteristics we have a data set with 20,850 individual firm-product-destination-year-firm characteristic observations over 2000-2003. The merged data used as the estimating sample contains 1,018 unique manufacturing firms. Although we were able to match more firms, several were dropped from the sample because they were not manufacturing firms (e.g., wholesalers), had incomplete information (e.g., missing input information in Prowess or TIPs), or did not survive our procedures to clean the data as described in the text and in this appendix.[31]

Appendix Table A.1: Probability of Dominant Unit Observations

A.1.A. Linear Probability Model Estimation

Independent Variable	Coef.	Robust Std. Err.	t	P>\|t\|
loggdppc	0.003	0.003	0.82	0.415
loggdp	0.000	0.003	0.13	0.893
logdist	0.013	0.006	2.01	0.045
logremote	-0.004	0.007	-0.60	0.548
logtfp	-0.021	0.010	-2.09	0.036
logklabor	-0.001	0.008	-0.14	0.893
loglabor	0.012	0.004	2.69	0.007
constant	0.778	0.091	8.55	0.000
n	26,903
R²	0.4809
Root MSE	0.36642

A.1.B. Probit Estimation

Independent Variable	Coef.	Robust Std. Err.	t	P>\|t\|
loggdppc	0.015	0.013	1.14	0.254
loggdp	0.001	0.010	0.09	0.931
logdist	0.065	0.026	2.51	0.012
logremote	-0.022	0.031	-0.72	0.471
logtfp	-0.082	0.033	-2.52	0.012
logklabor	-0.007	0.023	-0.31	0.759
loglabor	0.047	0.014	3.29	0.001
constant	-0.681	0.950	-0.72	0.473
n	13,073
Pseudo-R²	0.1726

Dependent Variable = 1 if a firm-product-destination-year observation is measured in the dominant unit for its product; 0 otherwise. Both regressions include product and year fixed effects, not reported.

2. Definition and construction of independent variables used in regressions.

We calculate TFP using the Stata implementation of the Levisohn and Petrin (2003) technique, following Topolova and Khandelwal’s (2011) approach (pp.998 $-$ 999) to put each firm’s productivity into index form (which itself depends on Aw, Chen and Roberts, 2001), which allows productivity comparisons within and between industries. We measure firm output with value-added (Topolova and Khandelwal use sales). Capital is measured as the size of each firm’s gross fixed assets, and labor is proxied by the wage and salary bill (the number of employees is not included in Prowess). Note that this is the measure of labor used both in the TFP calculation and directly (in log form, “loglabor”) on the right hand side of our regressions reported in Table 6; we also calculate the capital/labor ratio used in the regressions (“logklabor”) from these capital and labor variables.

We estimate TFP at the 4-digit National Industrial Classification (NIC) code level where possible, and at the 3-digit level when necessary due to a small number of firms at the 4-digit level (less than 20). We use Prowess data on firms’ spending on raw materials and electric power as the proxy for productivity shocks. All variables are expressed in real terms: output is deflated by two-digit industry-level wholesale prices indices from Ahsan (2013); capital expenditures are deflated by a capital goods wholesale price index we construct from several sub-industry wholesale price indices (including machine tools, electric machinery, and other capital goods); materials and power are likewise deflated with separate materials and power wholesale price indices we construct; and finally the wage and salary bill is deflated by the Economist Intelligence Unit’s Indian labor cost index.

We calculate remoteness as in Harrigan, et al. (2015): the GDP-weighted distance of an export partner from all other export partners. So, for example, when we observe a transaction with the Philippines we sum the GDP-weighted distances between the Philippines and India’s other export partners. Therefore $R_{d} = {[\sum Y_{0} d i s t_{o d}^{- 1}]}^{- 1}$ , where R_dis the remoteness of country d, Y₀is the GDP of country 0, a member of the set of India’s trading partners, and dist_odis the distance between d and a given country 0.

References

Acemoglu, D. and F. Zilibotti. 2001. “Productivity Differences.” Quarterly Journal of Economics, 116, 563 $-$ 606.

Ahsan, R. 2013. “Input Tariffs, Speed of Contract Enforcement, and the Productivity of Firms in India.” Journal of International Economics, 90(1), 181 $-$ 192.

Alchian, A. and W. Allen. 1964. University Economics. Belmont, CA: Wadsworth.

Antoniades, A. 2015. “Heterogeneous Firms, Quality, and Trade.” Journal of International Economics, 95(2), 263 $-$ 273.

Aw, B., X. Chen, and M. Roberts. 2001. “Firm Level Evidence on Productivity Differentials and Turnover in Taiwanese Manufacturing.” Journal of Development Economics, 66(1), 61 $-$ 86.

Baldwin, R. and J. Harrigan. 2011. “Zeros, Quality, and Space: Trade Theory and Trade Evidence.” American Economic Journal: Microeconomics, 3(2), 60 $-$ 88.

Bardhan, P. 2010. Awakening Giants, Feet of Clay: Assessing the Economic Rise of China and India. Princeton, NJ: Princeton University Press.

Bastos, P. and J. Silva. 2010. “The Quality of a Firm’s Exports: Where You Export to Matters.” Journal of International Economics, 82(2), 99 $-$ 111.

Bernard, A., B. Jensen, S. Redding, and P. Schott. 2007. “Firms in International Trade.” Journal of Economic Perspectives, 21(3), 105 $-$ 130.

Besedes, T. and T. Prusa. 2011. “The Role of Extensive and Intensive Margins and Export Growth.” Journal of Development Economics, 96, 371 $-$ 379.

Dahlman, Carl J. 2007. “China and India: Emerging Technological Powers.” Issues in Science and Technology, 23(3).

Dougherty, Sean. 2007. “India and China: Making Sense of Innovation and Growth.” OECD Observer No. 264/265, December 2007-January 2008.

Eaton, J., M. Eslava, M. Kugler, and J. Tybout. 2008. “Export Dynamics in Colombia: Firm-Level Evidence.” In E. Helpman, D. Marin and T. Verdier (ed.), The Organization of Firms in a Global Economy, Cambridge, MA: Harvard University Press.

Foster, L., J. Haltiwanger, and C. Syverson. 2008. “Reallocation, Firm Turnover and Efficiency: Selection on Productivity or Profitability?” American Economic Review, 98, 394 $-$ 425.

Goldberg, P., A. Khandelwal, N. Pavcnik, and P. Topalova. 2010a. “Multiproduct Firms and Product Turnover in the Developing World: Evidence from India.” Review of Economics and Statistics, 92(4), 1042 $—$ 1049.

Goldberg, P., A. Khandelwal, N. Pavcnik, and P. Topalova. 2010b. “Trade Liberalization and New Imported Inputs.” American Economic Review: Papers & Proceedings, 99(2), 494 $-$ 500.

Görg, H., H. Laszlo, and B. Muraközy. 2010. “Why Do Within Firm-Product Export Prices Differ Across Markets?” Kiel Institute for the World Economy, Working Paper 1596 (February).

Hall, R. and C. Jones. 1999. “Why Do Some Countries Produce So Much More Output per Worker than Others?” Quarterly Journal of Economics, 114, 83 $-$ 116.

Harrigan, J. 1999. “Estimation of Cross-Country Differences in Industry Production Functions.” Journal of International Economics, 47, 267 $-$ 294.

Harrigan, J., X. Ma and V. Shlychkov. 2015. “Export Prices of U.S. Firms.” Journal of International Economics. Available online 14 May. doi:10.1016/j.jinteco.2015.04.007.

Head, K., T. Mayer, and J. Ries. 2010. “The Erosion of Colonial Trade Linkages After Independence.” Journal of International Economics, 81(1), 1 $-$ 14.

Hummels, D. and A. Skiba. 2004. “Shipping the Good Apples Out? An Empirical Confirmation of the Alchian-Allen Conjecture.” Journal of Political Economy, 112(6), 1384 $-$ 1402.

Khandelwal, A. 2010, “The Long and Short (of) Quality Ladders,” Review of Economic Studies, 77, 1450 $-$ 1476.

Kugler, M. and E. Verhoogen. 2012. “Prices, Plant Size, and Product Quality.” Review of Economic Studies, 79, 307 $-$ 339.

Levinsohn, J. and A. Petrin. 2003. “Estimating Production Functions Using Inputs to Control for Unobservables.” Review of Economic Studies, 70, 317 $-$ 341.

Manova, K. and Z. Zhang. 2012. “Export Prices Across Firms and Destinations.” The Quarterly Journal of Economics, 127, 379 $-$ 436.

Martin, J. 2012. “Markups, Quality and Transport Costs.” European Economic Review, 56, 777 $-$ 791.

Melitz, M. 2003. “The Impact of Trade on Intra-Industry Reallocations and Aggregate Industry Productivity.” Econometrica, 71(6), 1695 $-$ 1725.

Melitz, M. and G. Ottaviano. 2008. “Market Size, Trade, and Productivity.” Review of Economic Studies, 75, 295 $-$ 316.

Panagariya, A. 2008. India: The Emerging Giant. New York: Oxford University Press.

Rauch, J. 1999. “Networks versus Markets in International Trade.” Journal of International Economics, 48, 7 $-$ 35.

Roberts, M. and D. Supina. 1996. “Output Price, Markups, and Producer Size.” European Economic Review, 40, 909 $-$ 921.

Roberts, M. and D. Supina. 2000. “Output Price and Markup Dispersion in Micro Data: The Roles of Producer Heterogeneity and Noise.” In Baye, M. (ed.), Advances in Applied Microeconomics, 9, 1 $-$ 36. Amsterdam: JAI.

Roy, J. 2002. “Towards International Norms for Indirect Taxes and Trade Facilitation in India.” Background paper prepared for the Task Force on Indirect Taxes, Government of India, New Delhi.

Roy, J. and S. Bagai. 2005. “Key Issues in Trade Facilitation: Summary of World Bank/EU Workshops in Dhaka and Shanghai in 2004.” World Bank Policy Research Working Paper No. 3703.

Sutton, J. 1998. Technology and Market Structure: Theory and History. Cambridge: MIT Press.

Syverson, C. 2007. “Prices, Spatial Competition, and Heterogeneous Producers: An Empirical Test.” Journal of Industrial Economics, 55, 197 $-$ 222.

Tian, Wei and M. Yu. 2012. “China and India: Trends in Trade Over the Last Decade.” The Journal of China and Global Economics, 1(1), 27 $-$ 38.

Topalova, P. and A. Khandelwal. 2011. “Trade Liberalization and Firm Productivity: The Case of India.” The Review of Economics and Statistics, 93(3), 995 $-$ 1009.

Trefler, D. 1993. “International Factor Price Differences: Leontief Was Right!” Journal of Political Economy, 101, 961 $-$ 987.

Türkcan, K. 2014. “Investigating the role of Extensive Margin, Intensive Margin, Price and Quantity Components on Turkey’s Export Growth During 1998-2011.” MPRA Paper No. 53292.

Wooldridge, J. 1995. “Selection Corrections for Panel Data Models Under Conditional Mean Independence Assumptions.” Journal of Econometrics, 68(1), 115 $-$ 132.

[1] Khandelwal (2010) discusses the difference between heterogeneous and homogeneous markets.

[2] See, for example, Bardhan (2010) for an extensive comparison.

[3] In Antoniades (2015) the scope for quality differentiation (λ) is dependent on market size (L), product substitutability (1/γ), the cost of innovation (θ), and β and δ, where λ=L(β-δ)/(4θγ-L(β-δ)²). The scope for quality differentiation is increasing in market size, and decreasing in product substitutability and the cost of innovation. For the case of homogeneous goods then γ approaches infinity and the scope for product differentiation becomes zero.

^{^[4]} Manova and Zhang (2012, p.2) present evidence that not only do successful exporters produce higher quality goods (with higher quality inputs), but that firms adjust product quality according to characteristics of the destination market. In particular, they find that the higher unit values associated with higher distance to destination markets and with serving more destinations are due to compositional shifts within narrow product categories towards higher product quality and higher quality inputs.

^{^[5]} Indian fiscal years run from April 1 through March 31; the actual data run from April 1999 through March 2003. All told, TIPS records more than 5.8 million export transactions over this period.

[6] So, for example, if curry powder had most of its export value in kilos then we analyze only those observations, losing (say) exports measured in boxes.

^{^[7]} Previous firm-level research for India using the Prowess database include Goldberg, Khandelwal, Pavnik and Topolova (2010b), Topolova and Khandelwal (2011), and Ahsan (2013).

^{^[8]} This trade-by-enterprise-characteristics database is part of a wider effort by USITC staff to examine trade and firm dynamics in the context of rapidly emerging economies.

^{^[9]} See the appendix for details on the merge.

^{^[11]} U.S. information referenced here and in the previous paragraph is from Bernard, Jensen, Redding, and Schott (2007), pp. 116-8.

^{^[12]} Fine-grained product and destination data allow latitude in defining “existing” and “new” markets. For instance, is it an extensive or intensive change when a firm that has been exporting a good to one destination begins selling the same good to another destination? Or when a firm resumes sales to a destination after a year’s hiatus? The trade literature offers no consensus for decomposing revenue changes into their intensive and extensive components, nor for decomposing changes on the intensive and extensive margins into price and quantity components. “Count” methods remain popular though not dominant. See Besedes and Prusa (2011), Türkcan (2014), and Eaton, Eslava, Kugler, and Tybout (2008).

[13] These calculations use nominal prices, but the mild inflation over the period of our sample should not affect the main conclusions.

[14] A given firm-product pair may be represented in this data up to three times (2001, 2002, and 2003). Note that its weighted average price change may switch signs from year to year, and, since it is an annual weighted average across destinations, may be negative even if prices are rising in one or more destinations.

^{^[15]} See the appendix for details on the construction of our variables.

[16] See Appendix for details on variable definitions and construction.

^{^[17]} The Wooldridge (2015) approach would fit a Tobit regression of revenues in the expanded data with zero revenues. The residuals from this estimation would then be used to control for selection bias in the price regressions.

^{^[18]} In results not reported here we employ the Wooldridge (2015) selection correction. Results are similar in magnitude, though statistical significance is weaker for destination country characteristics.

^{^[19]} In results not reported we examined how our results changed: (1) with the exclusion of firm characteristics beyond TFP, excluding individually and together our measure of firm size (loglabor) and the capital to labor ratio (logklabor); and, separately, (2) with the inclusion of firm-product fixed effects replacing our product fixed effects. For (1) all results, including those for TFP, distance, and remoteness, were robust to the exclusion of any combination of loglabor and logklabor. For (2) all results are robust except for TFP, which loses statistical significance. We suspect that the TFP result reflects the product-firm fixed effects controlling for much of the cross-sectional variation in firm prices.

[20] Calculated as follows: mean TFP is 126.4, with standard deviation of 84.8, so (84.8/126.4)*100*(-0.162) = -10.86.

^{^[21]} These results are not reported here, but are available from the authors.

[22] Statistics calculated using Comtrade and World Development Indicators. Further, over the period 2001 2005 India’s share of world trade remained constant at one percent while China’s increased from four percent to seven percent (Tian and Yu, 2012).

[23] Further, Roy and Bagai (2005) found that the time taken for exports to move out of India at Delhi airport was 2.5 days (international norm is 12 hours) and at Mumbai port was 3 5 days (norm is less than 18 hours).

[24] For example, a firm beginning to engage in R&D knows that it will be difficult to redeploy resources if the project is not successful, a cost which must be taken into account when considering whether or not to undertake the activity.

[25] Data from the World Development Indicators tables

[26] We have R&D expenditure in manufacturing for China over 2008-2010 from the OECD, and expenditure on R&D in manufacturing, construction, electricity, gas and water over a similar period in India from the Open Government Data India platform. To calculate the shares we use information from the World Bank tables to calculate the size of the manufacturing sectors in China and India over this period. Given the broader R&D category for India, the share of R&D in manufacturing for India is overestimated.

^{^[27]} As a robustness check we also examine the conditioned correlations for the differentiated goods in the textiles and all other goods groups. We find here that the coefficients are negative, although less so than for machines, and insignificant due to the smaller sample sizes of these finer divisions. The results referenced in this paragraph and in this footnote are not reported here although they are available from the authors.

^{^[28]} The entire list of key words is: Exporter, Importer, Trading, Trader, Export, Import, IMPEX, and EXIM.

^{^[29]} In brief, here is how we obtained that information: Within each of the 16,109 8-digit categories, the median number of (reported) individual product lines is 8, and the mean is 166. In some cases the product-level labels are variants of names for the same product, differing only in punctuation, capitalization, or word order. Sometimes these differences are present along with changes in the product description; thus we may see “Curry Powder” and “SPICE CURRYPOWDER” describing what appear to be the same product. By contrast, in other cases the product names reflect substantively different products within a particular HS line. We used a computerized matching algorithm to match product names, to say (in the example above) that “Curry Powder” and “ SPICE CURRYPOWDER” are the same product, but “Curry Powder” and “Ginger” are different products, even though all of these are inside the same HS-8 code. We then aggregate together the quantity and value information for those product labels that our algorithm deems as the same product (from the same firm).

[30] As a further check we also examined two cross tabs. The first is a cross tab of total export values in dominant and non-dominant units against firm TFP. The second is a cross tab of export values against distance to destination market. In each cross tab the cell percentages (in dominant vs. non-dominant quantity units) are quite similar. This simple descriptive analysis supports the results in the LPM and the Probit; the cross tabs are not reported here but are available from the authors.

[31] To provide an idea of how the two databases overlap, out of 5,235 manufacturing firms in Prowess during our period of analysis, we were able to match 1,986 firms with the trade data. We believe this is a relatively good merge, especially given the fact that many manufacturing firms do not export.