THE EFFECTS OF TARIFFS ON EMPLOYMENT
IN GLOBAL VALUE CHAINS

Andre Barbe

David Riker

ECONOMICS WORKING PAPER SERIES

Working Paper 2017-07-A

U.S. INTERNATIONAL TRADE COMMISSION

500 E Street SW

Washington, DC 20436

April 2017

The authors are grateful to Dan Kim and James Stamps for helpful comments and suggestions.

Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research.

The Effects of Tariffs on Employment in Global Value Chains

Andre Barbe and David Riker

Office of Economics Working Paper 2017-07-A

July 2017

ABSTRACT

We develop a two-country model of international trade and domestic employment in an industry with firm heterogeneity and global value chains. The model can be used to simulate the changes in trade and employment that would result from a tariff or other barrier to trade that increases the price of imports. We also identify the data that is needed to apply the model to a specific industry. As an example application, we use the model to simulate the effects of a hypothetical import barrier that raises the price of imports by 10 percent. We find that the import barrier would have a positive effect on domestic employment in the part of the industry that sells final products in the domestic market because it limits import competition. On the other hand, the import barrier would have a negative effect on employment in the part of the domestic industry that exports intermediate products for further manufacture before returning to the domestic market. The net effect on domestic employment $-$ whether it increases or decreases $-$ depends on many economic attributes of the industry, including its pattern of global value chains.

Keywords: global value, chains, global supply chains, offshoring, employment, international trade

JEL Codes: F16, F12, F23

Andre Barbe

Office of Economic, Research Division

Andre.Barbe@usitc.gov

David Riker

Office of Economics, Research Division

David.Riker@usitc.gov

1 Introduction

Several manufacturing industries are well-known for their global value chains, including the motor vehicles, textiles and apparel, and electronics industries. In these industries, it is possible to split the production process into different stages and locate these production stages in different countries. Generally, the more technically advanced and capital-intensive production processes are located in advanced countries, while the more labor-intensive production processes and assembly are located in lower wage, developing countries. This pattern of linked, multinational production is often called offshoring.

In this paper, we analyze how tariffs or other barriers to the imports of an advanced country like the United States can interrupt these back-and-forth trade flows and thus affect employment within the global value chains. First and foremost, a tariff on the imports of the advanced country will have a positive effect on domestic employment in the import-competing part of the industry that sells the final product, because the tariff limits import competition. This positive effect on domestic employment provides the traditional motivation for protecting domestic industries by restricting imports. On the other hand, the tariff will also have a negative effect on domestic employment in the part of the industry that exports intermediate products. Since the demand for the advanced country’s exports of intermediate products is linked to the country’s demand for imports of further processed versions of these products, a barrier to one link in the supply chain can have a ripple effect throughout the chain. However, is this second effect large enough to offset the traditional positive employment effects of protecting a domestic industry?

To address this question, we developed a theoretical model of trade in intermediate and final products with firm heterogeneity and global value chains. We show how the model can be used to estimate the change in industry employment that would result from a barrier to imports of the final product into the market of the advanced country.[1]

Then we identify the data that are needed to apply the model to a specific industry. The goal of our analysis is to highlight the attributes of the industry’s global value chain that are determinants of the magnitude, and even the direction, of the changes in industry employment in the advanced country. These data inputs include the share of domestic shipments that are competing with imports, the share of exports that return to the advanced country rather than serving foreign markets, and the substitutability between domestic and foreign products in the domestic market.

Our paper contributes to the economics literature that models the effects of global value chains and trade in intermediate goods (sometimes called offshoring) on labor markets. Our paper incorporates recent theoretical innovations in this area. Grossman and Rossi-Hansberg (2008) develop a theoretical model of international trade in tasks. Firms are able to split their production process into a continuum of distinct tasks and then decide where to locate each task, based on costs of trade and costs of multinational production. Grossman and Rossi-Hansberg use their model to predict how changes in trade costs affect the feasibility of offshoring and the wages of workers at different skill levels in different countries. They find that increased offshoring can lead to productivity benefits and higher labor demand in the Home country, especially less skilled workers.[2] Feenstra (2008, 2016) provides excellent summaries of this theoretical literature.[3] In addition, the analysis of multinational production in Helpman, Melitz, and Yeaple (2004) provides modeling structure that we are able to incorporate in our paper, though Helpman, Melitz, and Yeaple focus on foreign affiliates placed for proximity to the foreign market (horizontal FDI), while our model focuses on global value chains (vertical FDI).

The rest of our paper is organized into four parts. Section 2 presents the structure and assumptions of our modeling framework. Section 3 estimates the net employment effects for a wide range of potential data inputs. Section 4 discusses the data needed to apply the model to a specific industry. Section 5 offers concluding remarks.

2 Model Description

We have developed a modeling framework for estimating the changes in domestic employment if a tariff or other barrier were imposed on imports. The framework is based on the models of trade with firm heterogeneity in Melitz (2003) and Helpman, Melitz, and Yeaple (2004) and the model of offshoring in Grossman and Rossi-Hansberg (2008). In this section, we describe the assumptions of our model and the equations that characterize the market equilibrium. Then we derive how trade flows and industry employment would change in response to an increase in barriers to imports.

2.1 General Setup of the Model

The model focuses on a vertically integrated manufacturing industry. Firms in the industry produce differentiated final products. Labor is the only factor of production in the model, and producers vary in their unit labor requirements. The model includes two regions, Home and Foreign, indicated by subscripts $H$ and $F$ . These two regions are distinct consumer markets and also potential production sites. There are two stages of production in the model, manufacturing of intermediate products and then manufacturing of the final products. The final products are then consumed by households in each region. Each firm chooses the location of each stage of its production process and the location of its final market based on relative production and trade costs.[4]

In the model, the two potential regions for intermediate production, final production, and consumption define eight possible supply chains. We refer to each supply chain by a three-letter label, with the first letter indicating the location of intermediate production, the second the location of final production, and the third the location of consumption. However, some of these supply chains may not exist in particular industries. For example, we assume that FHH and FHF are not profitable alternatives in the industry. This would be the case, for example, if it were not cost effective to locate final production in Home unless the entire vertically integrated production process and the consumer are in Home. In this case, imports to Home are all final products and most exports from Home to Foreign are intermediate products. Based on this assumption, we omit the FHH and FHF supply chains from our model, leaving the six relevant supply chains in Figure 1.

Figure 1: Six Different Supply Chains

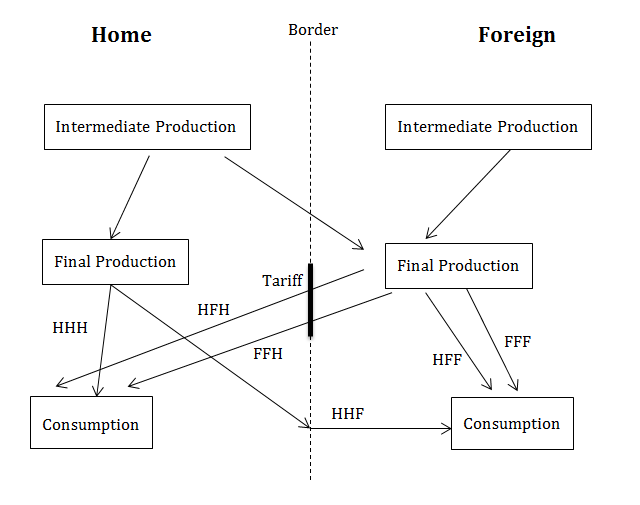
Title: This figures illustrates which of the different supply chains crosses the border and is affected by the tariff.

A new barrier to Home imports would impede the last link in the FFH and HFH supply chains. The reduction in HFH imports would reduce the demand for intermediate exports from Home. The reductions in FFH and HFH imports would increase the demand for domestic shipments (the HHH supply chain).[5]

We assume that there are $n_{H}$ potential Home producers and $n_{F}$ potential Foreign producers in the industry. Each firm produces a single variety of the good.[6] We assume that consumers have CES preferences between the varieties within the industry, and a unit elastic demand for the products of the industry in aggregate. The parameter $σ$ is the elasticity of substitution between the different varieties. The firms that produce the differentiated varieties engage in monopolistic competition.

2.2 Costs and Pricing

The costs of supplying each national market depend on the location of production. The unit labor requirement of each producer, $a$ , is drawn from a Pareto distribution with cumulative distribution function $G (a)$ , following Helpman, Melitz, and Yeaple (2004). In addition to the variable costs of production, there are variable costs of importing into Home and Foreign, represented by the gross trade cost factors $τ_{H}$ and $τ_{F}$ .[7] The trade cost factors could include tariffs and non-tariff measures as well as international transport costs. There are also fixed costs of establishing production in each region and fixed costs of trading intermediate and final products. The total fixed costs for each of the supply chains, summing all of the fixed cost components, are represented by $C_{H H H}$ , $C_{F F H}$ , $C_{H F H}$ , $C_{F F F}$ , $C_{H F F}$ , and $C_{H H F}$ . For example, $C_{H F H}$ includes the fixed costs of producing the intermediate products in Home, the fixed costs of exporting the intermediate products to Foreign, the fixed costs of final production in Foreign, and finally the fixed costs of exporting the final products to Home. We assume that the fixed costs and the variable trade costs use a combination of materials and labor from outside of the industry and non-production workers within the industry, but do not employ production workers within the industry.[8]

Production requires labor inputs in multiple stages. We simplify the model by only including two stages of production that are combined in fixed proportions.[9] Equation (1) represents the marginal cost of locating intermediate production in region $i$ and final production in region $j$ for a firm with unit labor requirement $a$ in the first stage of production and unit labor requirement $λ a$ in the second stage, and then delivering the final product to region $k$ .

$m c_{i j k} (a) = (w_{i} τ_{j} + λ w_{j}) τ_{k} a$ (1)

The variables $w_{i}$ and $w_{j}$ are the wage rates in the two regions. Equation (2) represents the demand for this product in region $k$ .

$q_{i j k} (a) = ϕ \frac{E_{k}}{P_{k}} {(\frac{p_{i j k} (a)}{P_{k}})}^{- σ}$ (2)

The variable $E_{H}$ represents the aggregate expenditure level in Home, $P_{H}$ is the CES price index for the industry in Home, and $ϕ$ is the expenditure share on the products of the industry. The model assumes that the industry or sector receives a constant share of aggregate expenditures, corresponding to Cobb-Douglas preferences across the products of the different sectors of the economy. This is a common assumption in multi-sector models of international trade. It implies that the price elasticity of the composite product of the industry is equal to minus one.

The firms in the industry set prices to maximize profits, taking the industry price index as given. The CES demand and monopolistic competition imply the constant mark-up pricing in equation (3).

$p_{i j k} (a) = \frac{σ}{σ - 1} m c_{i j k} (a)$ (3)

2.3 Firm Revenue and Profits

Similar to costs, firms have different revenues and profits depending on which supply chain they use. Equation (4) represents the revenue in the Home market of a domestic firm with unit labor requirement $a$ and completely domestic production (an HHH supply chain), and equation (5) represents the firm’s profits from this revenue stream.

$R_{H H H} (a) = ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ) a)}^{1 - σ}$ (4)

$π_{H H H} (a) = \frac{1}{σ} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ) a)}^{1 - σ} - C_{H H H}$ (5)

Equations (6) through (10) are the profits associated with the other five supply chains in Figure 1.

$π_{H F H} (a) = \frac{1}{σ} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} (w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H}) a)}^{1 - σ} - C_{H F H}$ (6)

$π_{F F H} (a) = \frac{1}{σ} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ) τ_{H} a)}^{1 - σ} - C_{F F H}$ (7)

$π_{F F F} (a) = \frac{1}{σ} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ) a)}^{1 - σ} - C_{F F F}$ . (8)

$π_{H F F} (a) = \frac{1}{σ} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} (w_{H} τ_{F} + λ w_{F}) a)}^{1 - σ} - C_{H F F}$ (9)

$π_{H H F} (a) = \frac{1}{σ} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ) τ_{F} a)}^{1 - σ} - C_{H H F}$ (10)

2.4 Productivity Cutoffs

Different firms will serve different supply chains, depending on whether their productivity is above or below certain productivity cutoffs. All firms in Home with unit labor requirements below $a_{H H H}$ supply the Home market, either through completely domestic production (an HHH supply chain) or by offshoring the final stage of production (an HFH supply chain). The cutoff unit labor requirement for a firm to supply the Home market is implicitly defined in equation (11).

$π_{H H H} (a_{H H H}) = 0$ (11)

Equations (5) and (11) imply the equilibrium cutoff level $a_{H H H}$ in equation (12).

$a_{H H H} = {(\frac{σ C_{H H H}}{ϕ E_{H}})}^{\frac{1}{1 - σ}} \frac{P_{H}}{w_{H} (1 + λ)} (\frac{σ - 1}{σ})$ (12)

Firms with unit labor requirements below a second cutoff $a_{H F H}$ , defined in equations (13) and (14), supply Home by offshoring the final stage of production.

$π_{H F H} (a_{H F H}) - π_{H H H} (a_{H F H}) = 0$ (13)

$a_{H F H} = {(\frac{σ (C_{H H H} - C_{H F H})}{ϕ E_{H}})}^{\frac{1}{1 - σ}} P_{H} {({(w_{H} (1 + λ))}^{1 - σ} - {((w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H}))}^{1 - σ})}^{\frac{1}{σ - 1}} (\frac{σ - 1}{σ})$ (14)

We assume that $C_{H H H}$ is less than $C_{H F H}$ , since offshoring incurs additional fixed costs, and therefore $a_{H F H}$ is less than $a_{H H H}$ . The most productive firms offshore their final production stage.

Equations (15) and (16) define the cutoff unit labor requirements for Foreign firms to export to Home.

$π_{F F H} (a_{F F H}) = 0$ (15)

$a_{F F H} = {(\frac{σ C_{F F H}}{ϕ E_{H}})}^{\frac{1}{1 - σ}} \frac{P_{H}}{w_{F} (1 + λ) τ_{H}} (\frac{σ - 1}{σ})$ (16)

Likewise, equations (17) through (22) define the cutoff unit labor requirements for supplying Foreign through each of the alternative supply chains.

$π_{F F F} (a_{F F F}) = 0$ (17)

$a_{F F F} = {(\frac{σ C_{F F F}}{ϕ E_{F}})}^{\frac{1}{1 - σ}} \frac{P_{F}}{w_{F} (1 + λ)} (\frac{σ - 1}{σ})$ (18)

$π_{H F F} (a_{H F F}) - π_{H H F} (a_{H F F}) = 0$ (19)

$a_{H F F} = {(\frac{σ (C_{H F F} - C_{H H F})}{ϕ E_{F}})}^{\frac{1}{1 - σ}} P_{F} (\frac{σ - 1}{σ}) {({(w_{H} (1 + λ) τ_{F})}^{1 - σ} - {(w_{H} τ_{F} + λ w_{F})}^{1 - σ})}^{\frac{1}{σ - 1}}$ (20)

$π_{H H F} (a_{H H F}) = 0$ (21)

$a_{H H F} = {(\frac{σ C_{H H F}}{ϕ E_{F}})}^{\frac{1}{1 - σ}} \frac{P_{F}}{w_{H} (1 + λ) τ_{F}} (\frac{σ - 1}{σ})$ (22)

We assume that $C_{H H F}$ is less than $C_{H F F}$ , since offshoring incurs additional fixed costs, and therefore $a_{H F F}$ is less than $a_{H H F}$ . Again, the most productive firms offshore their final production stage.

2.5 Sales and Prices

The equilibrium value of sales (trade flows) for each supply chain and the overall price indices can be expressed in 3 different ways, depending on which variables you prefer it to be a function of.

2.5.1 Sales and Prices as a Function of Unit Labor Requirements and the Distribution of Productivities

Equations (23) through (25) represent the equilibrium values of sales in Home for each of the supply chains that serve that market, as a function of the cutoff unit labor requirements above and the distribution of unit labor requirements $G (a)$ .

$V_{H H H} = n_{H} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ))}^{1 - σ} \int_{a_{H F H}}^{a_{H H H}} a^{1 - σ} d G (a)$ (23)

$V_{H F H} = n_{H} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} (w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H}))}^{1 - σ} \int_{0}^{a_{H F H}} a^{1 - σ} d G (a)$ (24)

$V_{F F H} = n_{F} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ) τ_{H})}^{1 - σ} \int_{0}^{a_{F F H}} a^{1 - σ} d G (a)$ (25)

Equation (26) represents the corresponding CES price index in Home.

$P_{H} = (\frac{σ}{σ - 1}) {(n_{H} {(w_{H} (1 + λ))}^{1 - σ} \int_{a_{H F H}}^{a_{H H H}} a^{1 - σ} d G (a) + n_{H} {((w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H}))}^{1 - σ} \int_{0}^{a_{H F H}} a^{1 - σ} d G (a) + n_{F} {(w_{F} (1 + λ) τ_{H})}^{1 - σ} \int_{0}^{a_{F F H}} a^{1 - σ} d G (a))}^{\frac{1}{1 - σ}}$ (26)

Equations (27) through (29) represent the equilibrium values of sales in Foreign for each of the alternative supply chains that serve that market.

$V_{F F F} = n_{F} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ))}^{1 - σ} \int_{0}^{a_{F F F}} a^{1 - σ} d G (a)$ (27)

$V_{H F F} = n_{H} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} (τ_{F} w_{H} + λ w_{F}))}^{1 - σ} \int_{0}^{a_{H F F}} a^{1 - σ} d G (a)$ (28)

$V_{H H F} = n_{H} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ) τ_{F})}^{1 - σ} \int_{a_{H F F}}^{a_{H H F}} a^{1 - σ} d G (a)$ (29)

Equation (30) represents the CES price index in Foreign.

$P_{F} = (\frac{σ}{σ - 1}) {(n_{F} {(w_{F} (1 + λ))}^{1 - σ} \int_{0}^{a_{F F F}} a^{1 - σ} d G (a) + n_{H} {(τ_{F} w_{H} + λ w_{F})}^{1 - σ} \int_{0}^{a_{H F F}} a^{1 - σ} d G (a) + n_{H} {(w_{H} (1 + λ) τ_{F})}^{1 - σ} \int_{a_{H F F}}^{a_{H H F}} a^{1 - σ} d G (a))}^{\frac{1}{1 - σ}}$ (30)

2.5.2 Sales and Prices as a Function of Unit Labor Requirements and the Distribution of Productivities’ Shape Parameter

Assuming that the unit labor requirements for individual varieties have a Pareto distribution with shape parameter $k > σ - 1 > 0$ , we can rewrite equations (23) through (30) as follows:

$V_{H H H} = n_{H} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ))}^{1 - σ} [{(a_{H H H})}^{k - (σ - 1)} - {(a_{H F H})}^{k - (σ - 1)}] (\frac{k}{k - (σ - 1)})$ (31)

$V_{H F H} = n_{H} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} (w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H}))}^{1 - σ} {(a_{H F H})}^{k - (σ - 1)} (\frac{k}{k - (σ - 1)})$ (32)

$V_{F F H} = n_{F} ϕ E_{H} P_{H}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ) τ_{H})}^{1 - σ} {(a_{F F H})}^{k - (σ - 1)} (\frac{k}{k - (σ - 1)})$ (33)

$P_{H} = (\frac{σ}{σ - 1}) {(\frac{k}{k - (σ - 1)})}^{\frac{1}{1 - σ}} {(n_{H} {(w_{H} (1 + λ))}^{1 - σ} [{(a_{H H H})}^{k - (σ - 1)} - {(a_{H F H})}^{k - (σ - 1)}] + n_{H} {(w_{H} τ_{F} τ_{H} + λ w_{F} τ_{H})}^{1 - σ} {(a_{H F H})}^{k - (σ - 1)} + n_{F} {(w_{F} (1 + λ) τ_{H})}^{1 - σ} {(a_{F F H})}^{k - (σ - 1)})}^{\frac{1}{1 - σ}}$ (34)

$V_{F F F} = n_{F} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{F} (1 + λ))}^{1 - σ} {(a_{F F F})}^{k - (σ - 1)} (\frac{k}{k - (σ - 1)})$ (35)

$V_{H F F} = n_{H} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} (w_{H} τ_{F} + λ w_{F}))}^{1 - σ} {(a_{H F F})}^{k - (σ - 1)} (\frac{k}{k - (σ - 1)})$ (36)

$V_{H H F} = n_{H} ϕ E_{F} P_{F}^{σ - 1} {(\frac{σ}{σ - 1} w_{H} (1 + λ) τ_{F})}^{1 - σ} [{(a_{H H F})}^{k - (σ - 1)} - {(a_{H F F})}^{k - (σ - 1)}] (\frac{k}{k - (σ - 1)})$ (37)

$P_{F} = (\frac{σ}{σ - 1}) {(\frac{k}{k - (σ - 1)})}^{\frac{1}{1 - σ}} {(n_{F} {(w_{F} (1 + λ))}^{1 - σ} {(a_{F F F})}^{k - (σ - 1)} + n_{H} {(w_{H} τ_{F} + λ w_{F})}^{1 - σ} {(a_{H F F})}^{k - (σ - 1)} + n_{H} {(w_{H} (1 + λ) τ_{F})}^{1 - σ} [{(a_{H H F})}^{k - (σ - 1)} - {(a_{H F F})}^{k - (σ - 1)}])}^{\frac{1}{1 - σ}}$ (38)

2.5.3 Sales and Prices as a Function of Unit Labor Requirements, the Distribution of Productivities’ Shape Parameter, and Z

Next, we can rewrite equations (31) through (38) in terms of the ratio of the cutoff unit labor requirements for the different supply chains and relative wages, using common terms $Z_{H}$ and $Z_{F}$ to simplify the notation.

$V_{H H H} = n_{H} Z_{H} {(1 + λ)}^{1 - σ} [1 - {(\frac{a_{H F H}}{a_{H H H}})}^{k - (σ - 1)}]$ (39)

$V_{H F H} = n_{H} Z_{H} {(τ_{F} τ_{H} + λ \frac{w_{F}}{w_{H}} τ_{H})}^{1 - σ} {(\frac{a_{H F H}}{a_{H H H}})}^{k - (σ - 1)}$ (40)

$V_{F F H} = n_{F} Z_{H} {(\frac{w_{F}}{w_{H}} (1 + λ) τ_{H})}^{1 - σ} {(\frac{a_{F F H}}{a_{H H H}})}^{k - (σ - 1)}$ (41)

$Z_{H} = ϕ E_{H} {(n_{H} {(1 + λ)}^{1 - σ} [1 - {(\frac{a_{H F H}}{a_{H H H}})}^{k - (σ - 1)}] + n_{H} {(τ_{F} τ_{H} + λ \frac{w_{F}}{w_{H}} τ_{H})}^{1 - σ} {(\frac{a_{H F H}}{a_{H H H}})}^{k - (σ - 1)} + n_{F} {(\frac{w_{F}}{w_{H}} (1 + λ) τ_{H})}^{1 - σ} {(\frac{a_{F F H}}{a_{H H H}})}^{k - (σ - 1)})}^{- 1}$ (42)

$V_{F F F} = n_{F} Z_{F} {(\frac{w_{F}}{w_{H}} (1 + λ))}^{1 - σ}$ (43)

$V_{H F F} = n_{H} Z_{F} {(τ_{F} + λ \frac{w_{F}}{w_{H}})}^{1 - σ} {(\frac{a_{H F F}}{a_{F F F}})}^{k - (σ - 1)}$ (44)

$V_{H H F} = n_{H} Z_{F} {((1 + λ) τ_{F})}^{1 - σ} [{(\frac{a_{H H F}}{a_{F F F}})}^{k - (σ - 1)} - {(\frac{a_{H F F}}{a_{F F F}})}^{k - (σ - 1)}]$ (45)

$Z_{F} = ϕ E_{F} {(n_{F} {(\frac{w_{F}}{w_{H}} (1 + λ))}^{1 - σ} + n_{H} {(τ_{F} + λ \frac{w_{F}}{w_{H}})}^{1 - σ} {(\frac{a_{H F F}}{a_{F F F}})}^{k - (σ - 1)} + n_{H} {((1 + λ) τ_{F})}^{1 - σ} [{(\frac{a_{H H F}}{a_{F F F}})}^{k - (σ - 1)} - {(\frac{a_{H F F}}{a_{F F F}})}^{k - (σ - 1)}])}^{- 1}$ (46)

2.6 Effect of Import Costs on the Value of Trade Flows

Finally, we use the equilibrium conditions in equations (39) through (46) to calculate the percentage changes in economic outcomes in response to the increase in import costs in Home. For this calculation, we assume that wages and aggregate expenditure levels do not change with the industry-specific increase in import costs. Producer prices also do not change, since they are at a constant mark-up over marginal costs. This partial equilibrium approach is an appropriate simplifying assumption for an industry that is small relative to the aggregate national economies. In this case, and assuming that there is no change in the costs of importing into Foreign ( ${\hat{τ}}_{F} = 0$ ), there is no change in the global chains that supply Foreign.

${\hat{V}}_{F F F} = {\hat{V}}_{H F F} = {\hat{V}}_{H H F} = {\hat{Z}}_{F} = 0$ (47)

On the other hand, there are adjustments in the global value chains that supply Home, represented in percentage changes in equations (48) through (53). To simplify the notation, we define Home market shares $β_{i j H} \equiv V_{i j H} / (V_{H F H} + V_{H H H} + V_{F F H})$ for regions $i$ and $j$ , and the ratios of the cutoff unit labor requirements for supplying Home $r_{i j H} \equiv a_{i j H} / a_{H H H}$ .[10]

${\hat{V}}_{H H H} = {\hat{Z}}_{H} - (\frac{β_{H F H}}{β_{H H H}}) {(\frac{τ_{F} τ_{H} + λ τ_{H} (\frac{w_{F}}{w_{H}})}{1 + λ})}^{σ - 1} (k - (σ - 1)) {\hat{r}}_{H F H}$ (48)

${\hat{V}}_{H F H} = {\hat{Z}}_{H} + (1 - σ) {\hat{τ}}_{H} - (k - (σ - 1)) {\hat{r}}_{H F H}$ (49)

${\hat{V}}_{F F H} = {\hat{Z}}_{H} + (1 - σ) {\hat{τ}}_{H} - (k - (σ - 1)) {\hat{r}}_{F F H}$ (50)

${\hat{Z}}_{H} = (k - (σ - 1)) (β_{H F H} [{(\frac{τ_{F} τ_{H} + λ τ_{H} (\frac{w_{F}}{w_{H}})}{1 + λ})}^{σ - 1} - 1] {\hat{r}}_{H F H} - β_{F F H} {\hat{r}}_{F F H}) - (1 - σ) (β_{H F H} + β_{F F H}) {\hat{τ}}_{H}$ (51)

The cutoff unit labor requirements in equation (12), (14), and (16) imply the following changes in $r_{F F H}$ and $r_{H F H}$ in response to the increase in import costs:

${\hat{r}}_{F F H} = - {\hat{τ}}_{H}$ (52)

${\hat{r}}_{H F H} = (\frac{{(τ_{F} τ_{H} + λ (\frac{w_{F}}{w_{H}}) τ_{H})}^{1 - σ}}{{(1 + λ)}^{1 - σ} - {(τ_{F} τ_{H} + λ (\frac{w_{F}}{w_{H}}) τ_{H})}^{1 - σ}}) {\hat{τ}}_{H}$ (53)

The increase in import costs can lead to significant restructuring of the global value chains of the industry, including a change in whether some firms offshore. In the terminology of the literature on trade with firm heterogeneity, there are adjustments on the extensive margin of trade as well as the intensive margin of trade.

2.7 Effect on the Employment of Production Workers in Home

The increase in import costs does not change the value of sales in Foreign ( $V_{H H F}$ and $V_{H F F}$ ) in the partial equilibrium analysis, but it does change the value of sales in Home ( $V_{H H H}$ and $V_{H F H}$ ). In the model, the labor income of production workers in the HHH supply chain is a fixed fraction of $V_{H H H}$ , given the fixed mark-up of price over wages.[11]

$V_{H H H} = (\frac{σ}{σ - 1}) w_{H} L_{H H H}$ (54)

Equation (54) implies the following equation for Home employment of production workers in this purely domestic supply chain:

$L_{H H H} = \frac{V_{H H H}}{w_{H}} (\frac{σ - 1}{σ})$ (55)

Therefore, the percentage change in Home employment of production workers in the HHH supply chain is equal to the percentage change in $V_{H H H}$ , since wages do not adjust in the partial equilibrium analysis.

${\hat{L}}_{H H H} = {\hat{V}}_{H H H}$ (56)

Likewise, the labor income of Home production workers in the HFH supply chain is a fixed fraction of revenue in that supply chain, given the fixed mark-ups and the assumption that there are fixed factor proportions in production:

$V_{H F H} = (\frac{σ}{σ - 1}) (w_{H} τ_{F} + λ w_{F}) τ_{H} L_{H F H}$ (57)

Equation (57) implies the following equation for Home employment of production workers in the HFH supply chain:

$L_{H F H} = \frac{V_{H F H}}{(w_{H} τ_{F} + λ w_{F}) τ_{H}} (\frac{σ - 1}{σ})$ (58)

Therefore, the percentage change in Home employment of production workers in the HFH supply chain is equal to the percentage change in $V_{H F H}$ minus the percent change in $τ_{H}$ .

${\hat{L}}_{H F H} = {\hat{V}}_{H F H} - {\hat{τ}}_{H}$ (59)

According to the accounting identity in equation (60), the percentage change in total employment of production workers in Home is a share-weighted average of the percentage changes in the production workers employed in the two affected supply chains.

${\hat{L}}_{H} = (\frac{L_{H H H}}{L_{H}}) ({\hat{L}}_{H H H}) + (\frac{L_{H F H}}{L_{H}}) ({\hat{L}}_{H F H})$ (60)

Equation (61) substitutes equations (56) and (59) into equation (60).

${\hat{L}}_{H} = (\frac{L_{H H H}}{L_{H}}) ({\hat{V}}_{H H H}) + (\frac{L_{H F H}}{L_{H}}) ({\hat{V}}_{H F H} - {\hat{τ}}_{H})$ (61)

Finally, we approximate the employment shares in equation (61) using the status quo values of several industry statistics.[12]

${\hat{L}}_{H} = ω_{H} (1 - α_{H}) ({\hat{V}}_{H H H}) + (α_{H} γ_{H} δ_{H}) ({\hat{V}}_{H F H} - {\hat{τ}}_{H})$ (62)

The parameter $ω_{H}$ represents the share of Home’s domestic shipments (non-exports) that are competing directly with imports in the Home market, and the parameter $α_{H}$ represents the share of Home production that is exported. Our default assumption is that $ω_{H}$ is equal to $1 - α_{H}$ and all Home production is import-competing. However, we consider alternative assumptions in our sensitivity analysis of the model. The parameter $γ_{H}$ represents the share of exports from Home that are intermediate inputs into production within the same industry, and the parameter $δ_{H}$ represents the share of these exported intermediate products that return Home after further manufacturing in Foreign.

The net employment effect in equation (62) combines a positive effect on Home employment due to the increased demand for domestic shipments and a negative effect on Home employment due to the reduced demand for Home exports for further manufacture in Foreign and shipment back to the Home market.

3 Model Results

The model shows that the tariff has different effects on different supply chains. The increased import costs lead consumers to substitute to purely domestic producers, increasing employment in that supply chain. When a tariff is imposed ( ${\hat{τ}}_{H} > 0$ ), the model predicts that there will be an increase in domestic shipments ( ${\hat{V}}_{H H H} > 0$ ) and associated labor demand ( ${\hat{L}}_{H H H} > 0$ ). However, the tariff increases costs in supply chains that involve offshoring, and this has a negative effect on Home employment. More formally, the tariff leads to a reduction in exports of intermediates for reimport ( ${\hat{V}}_{H F H} < 0$ ) and associated labor demand ( ${\hat{L}}_{H F H} < 0$ ).

3.1 Example Simulation of the Model

We use simple numerical simulations to illustrate the magnitudes of the net employment effects for different values of the industry data that are inputs of the model. As a benchmark case, we assume that $α_{H} = 0.50$ , $β_{H F H} = 1 / 3$ , $β_{F F H} = 1 / 3$ , $β_{H H H} = 1 / 3$ , $γ_{H} = 0.9$ , $δ_{H} = 1 / 4$ , $ω_{H} = 1$ , $σ = 5$ , $λ = 1 / 2$ , $τ_{H} = 1$ , $τ_{F} = 1$ , $\frac{w_{F}}{w_{H}} = 1 / 2$ , and $k = 5$ .

The tariff has different effects on different supply chains. These effects are summarized in table 1. The tariff increases costs in the HFH and FFH supply chains. The sales of the competing HHH supply chain increase. This leads to an increase in the number of Home production workers in HHH and a decrease in the number of U.S. production workers in HFH. There is no Home employment in FFH, so there would be no impact there.

Table 1: Effect of the Tariff on Different Supply Chains

Supply Chain	Location of Intermediate Production	Location of Final Production	Location of Consumption	Supply Chain in the Model?	Change in Costs	Change in Domestic Employment
1 HHH	Home	Home	Home	Yes	None	Increase
2 HHF	Home	Home	Foreign	Yes	None	None
3 HFH	Home	Foreign	Home	Yes	Increase	Decrease
4 HFF	Home	Foreign	Foreign	Yes	None	None
5 FHH	Foreign	Home	Home	No	None	None
6 FHF	Foreign	Home	Foreign	No	None	None
7 FFH	Foreign	Foreign	Home	Yes	Increase	None
8 FFF	Foreign	Foreign	Foreign	Yes	None	None

If ${\hat{τ}}_{H} = 0.05$ (a 5% increase in import prices), then there is a 21 percent increase in the domestic shipments of Home producers ( ${\hat{V}}_{H H H} = 0.2132$ ) and an 11 percent increase in associated production workers ( ${\hat{L}}_{H H H} = 0.1066$ ). There is a 13 percent decline in imports from offshored final production ( ${\hat{V}}_{H F H} = - 0.1299$ ) and a 2 percent decline in associated production workers ( ${\hat{L}}_{H F H} = - 0.0202$ ). There is an almost 9 percent net increase in the total number of production workers in the industry in Home ( ${\hat{L}}_{H} = 0.0864$ .)

If all Home exports were final products that did not return to the Home market, then we would have only the positive effect from the increase in domestic shipments. However, since there is significant trade in intermediate products and offshoring in the example, then there is also a negative effect of the increase in import costs on the number of Home production workers.

3.2 Sensitivity Analysis

The values of different parameters affect the net change in industry employment. Table 2 lists the effects of each of the model’s parameters on net employment changes in the industry.

Table 2: Effects of the Model Parameters

Symbol	Baseline Value	Description	Effect of an Increase in the Parameter on the Net Employment Change
$α_{H}$	0.50	Home export share	Decrease
$β_{H H H}$	1/3	Domestic market share of supply chain HHH	Decrease
$β_{H F H}$	1/3	Domestic market share of supply chain HFH	Increase
$β_{F F H}$	1/3	Domestic market share of supply chain FFH	Increase
$γ_{H}$	0.9	Share of exports that are used as intermediate inputs	Decrease
$δ_{H}$	0.25	Share of Foreign production that re-enters the Home market	Decrease
$k$	5	Pareto shape parameter	Increase
$σ$	5	Consumer elasticity of substitution between each firms’ variety	Decrease
λ	0.5	Relative unit labor requirement in the final production stage	Decrease
$\frac{w_{F}}{w_{H}}$	0.5	Ratio of wages in Foreign and Home	Increase
$ω_{H}$	1	Share of Home’s domestic shipments that are import-competing	Increase

There is a specific reason why each of the parameters affects employment impacts in the manner it does. The net effect on Home employment in the industry is greater if its export share ( $α_{H}$ ) is small, because the negative effect on exports accounts for a small share of total industry employment. It is also greater if the import penetration ratios ( $β_{H F H}$ and $β_{F F H}$ ) are large or the domestic share is small ( $β_{H H H})$ , because the tariff provides more protection for the domestic industry, and this has a positive impact on industry employment. The net effect is greater if the share of exports that are used as intermediate inputs ( $γ_{H}$ ) and the share of these exports that returns to Home ( $δ_{H}$ ) are small, because the negative employment effect from the reduction in exports is less important. The net effect is greater if the Pareto shape parameter of the productivity distribution ( $k$ ) is large and the elasticity of substitution ( $σ$ ) is small, because trade flows are more sensitive to prices. It is greater if the relative unit labor requirement in the final stage of production (λ) is small or the ratio of the wage in Foreign to wage in Home ( $w_{F} / w_{H}$ ) is large, because under either of those conditions, the role for offshoring final production is less important. Finally, the net effect on industry employment is greater if the share of Home’s domestic shipments that are import-competing ( $ω_{H}$ ) is large, because this magnifies the positive effect of protection on employment from domestic shipments.

The net change in industry employment also depends on the time period being examined. The model addresses the firms’ decisions about whether to participate in different markets and where to locate the various stages of production. However, these adjustments on the extensive margins of trade do not occur immediately, and so the model can be best described as a model of long-run effects. However, the model can be easily converted to one of short-run effects, by assuming that there are no adjustments on the extensive margins and that there are no changes in the relative cut-off rules in equations (52) and (53). Omitting adjustments on the extensive margin reduces the absolute value of the modeled percentage net changes in industry employment. This implies that the net changes in employment are magnified by the adjustments on the extensive margins.

4 Data Requirements

Applying the model to a specific industry requires the following industry data:

· Market shares in the Home market

· Share of Home production that is exported

· Share of Home domestic shipments that are substitutes for the imported products

· Share of exports that are intermediate inputs subject to further processing

· Share of exports of intermediate inputs that return to Home

· Magnitude of initial variable trade costs

· Relative unit labor requirements of final production

· Wage in Foreign relative to the wage in Home

· Elasticity parameters $σ$ and ^$k$[13]

5 Conclusions

In this paper, we have developed an economic model of barriers to international trade in an industry with global value chains. We have derived from the model a relatively simple formula for employment effects that incorporates industry data on trade and production shares. The model demonstrates that there are positive and negative employment effects of impeding trade in global value chain, even within the same industry. The magnitudes of these effects, and even the sign of the net effect, will vary industry-by-industry depending on the data, and specifically the pattern of global value chains.

While the model focuses on employment effects, it can also be used to estimate the impact on the profitability of firms in the industry, for example to determine which firms are likely to gain or lose from the tariff. The sensitivity of each firm’s profits to the tariff depends on the firm’s global value chain, and specifically on the shares of $V_{H H H}$ , $V_{H F H}$ , and $V_{F F H}$ in its global sales, since the firm’s variable profits are proportional to its revenue in the model. If the firm supplies the Home market from all domestic production (an HHH supply chain), then it would unambiguously gain from the increase in import costs. On the other hand, if the firm supplies the Home market by offshoring some of its production (HFH and FFH supply chains), then it would generally lose from the increase in import costs. If the firm utilizes a mix of these three supply chains, then gains or losses will depend on the weights in the mix.

Extensions of the model that include additional countries and stages of production could be especially useful for evaluating the economic effects of changes in industry-specific rules of origin in trade agreements or for looking at industries which complex value chains that cross international borders many times before reaching consumers.

References

Antras, P. and E. Helpman (2004): “Global Sourcing.” Journal of Political Economy 112(3): 552-80.

Di Giovanni, J., A.A. Levchenko, and R. Rancière (2011): “Power Laws in Firm Size and Openness to Trade: Measurement and Implications.” Journal of International Economics 85: 42-52.

Feenstra, R.C. and G. Hanson (1999): “The Impact of Outsourcing and High-Technology Capital on Wages: Estimates for the U.S., 1979-1990” Quarterly Journal of Economics 114(3): 907-940.

Feenstra, R. C. (2008): “Offshoring in the Global Economy.” Ohlin Lecture at the Stockholm School of Economics.

Feenstra, R.C. (2016): Advanced International Trade, 2^nd Edition. Princeton, NJ: Princeton University Press.

Grossman, G.M. and E. Helpman (2005): “Outsourcing in a Global Economy.” Review of Economic Studies 72(1): 135-59.

Grossman, G.M. and E. Rossi-Hansberg (2008): “Trading Tasks: A Simple Theory of Offshoring.” American Economic Review 98 (5): 1978-97.

Helpman, E., M.J. Melitz, and S.R. Yeaple (2004): “Export Versus FDI with Heterogeneous Firms.” American Economic Review 94(1): 300-316.

Melitz, M. J. (2003): “The Impact of Trade on Aggregate Industry Productivity and Intra-Industry Reallocations.” Econometrica 71: 1695-1725.

Wright, G. (2014): “Revisiting the Employment Impact of Offshoring.” European Economic Review 66: 63-83.

[1] The model does not try to quantify the potential reductions in employment in other sectors of the economy if workers are drawn to a newly protected industry.

[2] Wright (2014) applies this model to a 2001-2007 panel dataset that includes a broad set of U.S. manufacturing industries. His measure of offshoring is the share of a U.S. industry’s intermediate inputs that are imported. He finds that a reduction in trade costs that increases offshoring had a negative direct displacement effect on U.S. employment but also a positive productivity effect.[2] He finds that the two effects mostly offset each other.

[3] Antras and Helpman (2004) and Grossman and Helpman (2005) are also important contributions to the literature on offshoring, though they focus on ownership structure and incomplete contracts rather than labor market impacts.

[4] The model focuses on the location of the different stages of production and the pattern of trade. It does not address ownership issues, e.g., the distinction between vertical integration and outsourcing of the production stages.

[5] In the context of our partial equilibrium model, there is no effect on supply chains that serve the foreign market.

[6] We assume that the firms have the technological capability to produce these varieties, but they may not find it profitable to participate in the market, given their firm-specific productivity. Their market participation decisions are explicitly addressed in the model.

[7] The gross trade cost factors are equal to one plus ad valorem charges.

[8] This assumption about inputs affects how we calculate the changes in the number of production workers.

[9] This assumption of complementarity in production is common in the trade literature on offshoring, including Feenstra and Hanson (1999).

[10] There are similar definitions for the market shares and ratios of cutoff levels for the other supply chains.

[11] This is the case because we have assumed that the fixed and variable trade costs involve a combination of materials and labor from outside of the industry and non-production workers within the industry, but not production workers within the industry.

[12] We assume that firms’ labor productivity is the same in their exports and domestic shipments.

[13] One data source for the Pareto shape parameter is Di Giovanni, Levchenko, and Rancière (2011). The authors estimate the parameter based on firm-level data on non-exporting French companies.